Question

复数z=log₂(x²-3x-3)+ilog₂(x-3),当x为何实数时,?

(1)z∈R;(2)z为虚数;(3)z为纯虚数??

Answer 1

思路分析:依照复数分类的条件求解此题,同时还要考虑实数x的范围.

解:(1)因为一个复数是实数的充要条件是虚部为零,?

所以有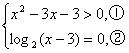

解②得x=4,经验证满足①.?

所以当x=4时,z∈R.?

(2)因为一个复数是虚数的充要条件是虚部不为零,所以有?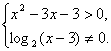

解得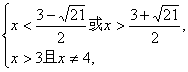

即＜x＜4或x＞4.?

所以当＜x＜4或x＞4时,z为虚数.?

(3)因为一个复数是纯虚数,则其实部为零且虚部不为零,?

所以有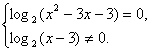

解得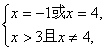

即x不存在.所以复数z不可能是纯虚数.