题目内容
(本小题满分14分)等差数列 的首项为
的首项为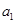 ,公差
,公差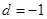 ,前
,前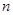 项和为
项和为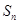 ,其中
,其中
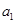
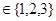 。
。
(Ⅰ)若存在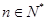 ,使
,使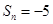 成立,求
成立,求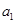 的值;
的值;
(Ⅱ)是否存在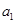 ,使
,使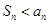 对任意大于1的正整数
对任意大于1的正整数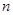 均成立?若存在,求出
均成立?若存在,求出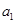 的值;否则,说明理由.
的值;否则,说明理由.
 的首项为
的首项为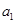 ,公差
,公差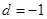 ,前
,前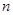 项和为
项和为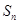 ,其中
,其中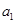
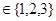 。
。(Ⅰ)若存在
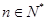 ,使
,使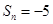 成立,求
成立,求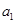 的值;
的值;(Ⅱ)是否存在
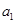 ,使
,使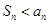 对任意大于1的正整数
对任意大于1的正整数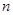 均成立?若存在,求出
均成立?若存在,求出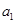 的值;否则,说明理由.
的值;否则,说明理由.(Ⅰ)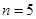 ;(Ⅱ)不存在
;(Ⅱ)不存在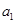 ,使
,使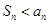 对任意大于1的正整数
对任意大于1的正整数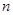 均成立 。
均成立 。
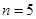 ;(Ⅱ)不存在
;(Ⅱ)不存在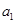 ,使
,使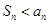 对任意大于1的正整数
对任意大于1的正整数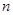 均成立 。
均成立 。本试题主要是考查了等差数列的前n项和与其通项公式之间的关系的转化。
(1)利用数列的前n项和公式可知得到首项与公差的关系式,那么可知结论。
(2)利用不等式关系,结合通项公式可知化简为关于n的不等式,然后讨论得到。
解:(Ⅰ)由条件得,
整理得: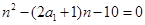
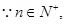 由求根公式
由求根公式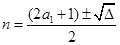 ,知
,知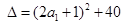 必为完全平方数,
必为完全平方数,
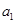
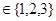 ,逐个检验知,
,逐个检验知,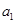 =1符合要求,此时
=1符合要求,此时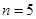 ;…………………………7分
;…………………………7分
(Ⅱ)由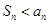 ,代入得
,代入得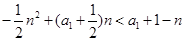
整理,变量分离得: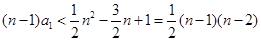
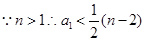
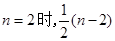 取到最小值
取到最小值 ,
,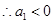
故不存在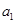 ,使
,使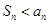 对任意大于1的正整数
对任意大于1的正整数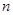 均成立 ………………… 14分
均成立 ………………… 14分
(1)利用数列的前n项和公式可知得到首项与公差的关系式,那么可知结论。
(2)利用不等式关系,结合通项公式可知化简为关于n的不等式,然后讨论得到。
解:(Ⅰ)由条件得,

整理得:
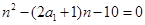
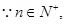 由求根公式
由求根公式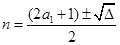 ,知
,知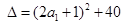 必为完全平方数,
必为完全平方数,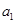
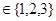 ,逐个检验知,
,逐个检验知,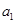 =1符合要求,此时
=1符合要求,此时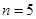 ;…………………………7分
;…………………………7分(Ⅱ)由
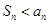 ,代入得
,代入得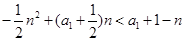
整理,变量分离得:
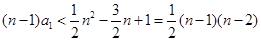
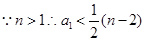
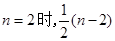 取到最小值
取到最小值 ,
,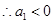
故不存在
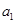 ,使
,使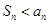 对任意大于1的正整数
对任意大于1的正整数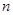 均成立 ………………… 14分
均成立 ………………… 14分
练习册系列答案
相关题目
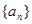 的通项公式为
的通项公式为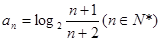 ,设其前n项和为Sn,
,设其前n项和为Sn,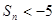 成立的自然数n( )
成立的自然数n( )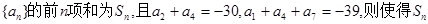 达到最小值的n是( )
达到最小值的n是( )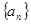 满足
满足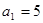 ,
,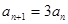 ,写出这个数列的前5项并归纳猜想通项公式。
,写出这个数列的前5项并归纳猜想通项公式。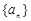 中,
中,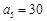 ,
,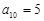 ,则
,则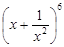 的展开式中的常数项是该数
的展开式中的常数项是该数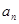 ﹜满足:
﹜满足: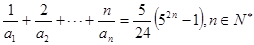 .(Ⅰ)求数列﹛
.(Ⅰ)求数列﹛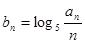 ,求
,求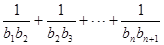
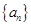 满足:
满足: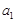 =
=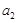 =2,
=2,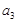 =3,
=3,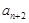 =
=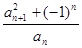 (
(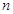 ≥2)
≥2)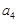 ,
,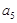 ,
,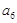 ;
;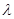 ,使得数列
,使得数列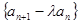 (
(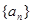 中,
中,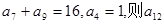 的值是( )
的值是( )