题目内容
已知正数数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]() (
(![]() ),
),
数列![]() 满足
满足![]()
(1)分别求![]() 和
和![]()
(2)设![]() ,数列
,数列![]() 的前
的前![]() 项和为
项和为![]() ,当
,当![]() 时,求证:
时,求证:![]()
(3)是否存在正整数![]() ,使得
,使得![]() 时,
时,![]() 恒成立?若存在,求出相应的
恒成立?若存在,求出相应的![]() 值,若不存在,请说明理由
值,若不存在,请说明理由
(1)当![]() 时,由已知得:
时,由已知得:![]() ,
,![]()
当![]() 时,
时,![]()
![]()
两式相减得:![]()
![]()
![]()
所以 ![]()
从而 ![]()
即 ![]() ……………… 5分
……………… 5分
(2)由(1)知![]()
所以 ![]()
因 ![]()
所以 ![]()
所以,由错位相减法得:
![]()
![]()
当![]() 时,
时,![]()
当![]() 时,
时,![]()
当![]() 时,
时,![]()
即当![]() 时,
时,![]()
所以当![]() 时,
时,![]()
即 ![]() ……………… 11分
……………… 11分
(3)假设存在正整数![]() ,使得
,使得![]() 时,
时,![]() 恒成立,即
恒成立,即![]() 恒成立
恒成立
当![]() 时,解得
时,解得![]() ,即当
,即当![]() 时,只要
时,只要![]() ,恒有
,恒有![]() 恒成立
恒成立
但当![]() 时,解得
时,解得![]() ,此时,不存在满足条件的
,此时,不存在满足条件的![]()
综上,故满足条件的![]() 不存在 ……………… 14分
不存在 ……………… 14分

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
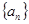 的前
的前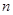 项和
项和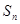 与通项
与通项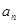 满足
满足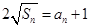 ,求
,求