题目内容
已知f(x)=loga (a>0,a≠1).
(a>0,a≠1).
(1)求函数f(x)的定义域;
(2)试判别函数f(x)的奇偶性,并说明理由;
(3)求使f(x)<0的x的取值范围.
解:(1)由f(x)=loga (a>0,a≠1)可得
(a>0,a≠1)可得  >0,即
>0,即 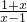 <0,即 (x+1)(x-1)<0,解得-1<x<1,
<0,即 (x+1)(x-1)<0,解得-1<x<1,
故函数f(x)的定义域为(-1,1).
(2)由于函数f(x)的定义域关于原点对称,且f(-x)=loga =loga
=loga 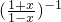 =-loga
=-loga  =-f(x),
=-f(x),
故函数f(x)是奇函数.
(3)f(x)<0,即 loga <0,当 0<a<1时,有
<0,当 0<a<1时,有  >1,即
>1,即 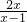 <0,即2x(x-1)<0,解得-1<x<1.
<0,即2x(x-1)<0,解得-1<x<1.
当a>1时,有 1> >0,∴
>0,∴ ,即
,即 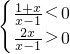 ,即
,即 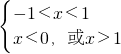 ,解得-1<x<0.
,解得-1<x<0.
综上可得,当 0<a<1时,使f(x)<0的x的取值范围为(-1,1);当a>1时,使f(x)<0的x的取值范围为(-1,0).
分析:(1)由函数的解析式可得 >0,即
>0,即 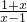 <0,即 (x+1)(x-1)<0,由此解得函数f(x)的定义域.
<0,即 (x+1)(x-1)<0,由此解得函数f(x)的定义域.
(2)由于函数f(x)的定义域关于原点对称,且f(-x)=-f(x),可得函数f(x)是奇函数.
(3)f(x)<0,即 loga <0,当 0<a<1时,当 0<a<1时,有
<0,当 0<a<1时,当 0<a<1时,有  >1,即
>1,即 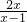 <0,即2x(x-1)<0,由此求得的x的取值范围.
<0,即2x(x-1)<0,由此求得的x的取值范围.
当a>1时,有 1> >0,故
>0,故  ,由此求出x的取值范围.
,由此求出x的取值范围.
点评:本题主要考查对数函数的定义域和值域,对数函数的单调性和特殊点,求函数的奇偶性的方法和步骤,属于中档题.
 (a>0,a≠1)可得
(a>0,a≠1)可得  >0,即
>0,即 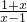 <0,即 (x+1)(x-1)<0,解得-1<x<1,
<0,即 (x+1)(x-1)<0,解得-1<x<1,故函数f(x)的定义域为(-1,1).
(2)由于函数f(x)的定义域关于原点对称,且f(-x)=loga
 =loga
=loga 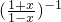 =-loga
=-loga  =-f(x),
=-f(x),故函数f(x)是奇函数.
(3)f(x)<0,即 loga
 <0,当 0<a<1时,有
<0,当 0<a<1时,有  >1,即
>1,即 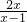 <0,即2x(x-1)<0,解得-1<x<1.
<0,即2x(x-1)<0,解得-1<x<1.当a>1时,有 1>
 >0,∴
>0,∴ ,即
,即 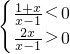 ,即
,即 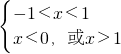 ,解得-1<x<0.
,解得-1<x<0.综上可得,当 0<a<1时,使f(x)<0的x的取值范围为(-1,1);当a>1时,使f(x)<0的x的取值范围为(-1,0).
分析:(1)由函数的解析式可得
 >0,即
>0,即 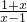 <0,即 (x+1)(x-1)<0,由此解得函数f(x)的定义域.
<0,即 (x+1)(x-1)<0,由此解得函数f(x)的定义域.(2)由于函数f(x)的定义域关于原点对称,且f(-x)=-f(x),可得函数f(x)是奇函数.
(3)f(x)<0,即 loga
 <0,当 0<a<1时,当 0<a<1时,有
<0,当 0<a<1时,当 0<a<1时,有  >1,即
>1,即 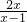 <0,即2x(x-1)<0,由此求得的x的取值范围.
<0,即2x(x-1)<0,由此求得的x的取值范围.当a>1时,有 1>
 >0,故
>0,故  ,由此求出x的取值范围.
,由此求出x的取值范围.点评:本题主要考查对数函数的定义域和值域,对数函数的单调性和特殊点,求函数的奇偶性的方法和步骤,属于中档题.

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目
已知f(x)是定义在R上的奇函数,当x>0时,f(x)=log
x,那么f(-
)的值是( )
| 1 |
| 4 |
| 1 |
| 2 |
A、
| ||
B、-
| ||
| C、2 | ||
| D、-2 |