题目内容
已知曲线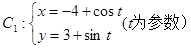 (t为参数),
(t为参数),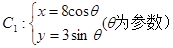
(1)化C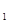 ,C
,C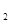 的方程为普通方程,并说明它们分别表示什么曲线;
的方程为普通方程,并说明它们分别表示什么曲线;
(2)若C 上的点P对应的参数为
上的点P对应的参数为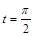 ,Q为C
,Q为C 上的动点,求
上的动点,求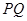 中点
中点 到直线
到直线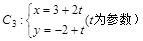 (t为参数)距离的最小值。
(t为参数)距离的最小值。
(1) ,表示圆;
,表示圆; ,表示椭圆(2)
,表示椭圆(2)
解析试题分析:解:(Ⅰ) ,
, ,
, 为圆心是(
为圆心是( ,半径是1的圆.
,半径是1的圆. 为中心是坐标原点,焦点在x轴上,长半轴长是8,短半轴长是3的椭圆.
为中心是坐标原点,焦点在x轴上,长半轴长是8,短半轴长是3的椭圆.
(Ⅱ)当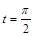 时,
时, 故
故
 为直线
为直线 ,
,
考点:参数方程与普通方程的转化
点评:要解决关于参数方程的问题,需将参数方程转化为直角坐标方程,然后再解决。而将参数方程转化为直角坐标方程,只需消去参数,但需考虑x和y的范围。

练习册系列答案
相关题目
某班有48名学生,在一次考试中统计出平均分为70分,方差为75,后来发现有2名同学的分数登错了,甲实得80分却记了50分,乙得70分却记了100分,更正后平均分和方差分别是( )
| A.70,75 | B.70,50 | C.70.1.04 | D.65,25 |
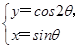 化为普通方程,并说明它表示的图形.
化为普通方程,并说明它表示的图形.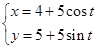 (t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ=2sinθ。
(t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ=2sinθ。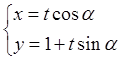 (t为参数,0 ≤ α < π).以原点为极点,x轴的正半轴为极轴建立极坐标系.已知曲线C的极坐标方程为ρcos2θ = 4sinθ.
(t为参数,0 ≤ α < π).以原点为极点,x轴的正半轴为极轴建立极坐标系.已知曲线C的极坐标方程为ρcos2θ = 4sinθ.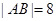 ,求α的值.
,求α的值.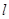 是过点
是过点 ,方向向量为
,方向向量为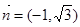 的直线。圆方程
的直线。圆方程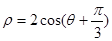
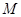 、
、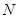 两点,求
两点,求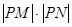 的值。
的值。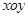 中,直线
中,直线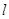 的方程为
的方程为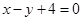 ,曲线
,曲线 的参数方程为
的参数方程为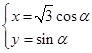 (
(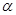 为参数)
为参数)  为极点,以
为极点,以 轴正半轴为极轴)中,点
轴正半轴为极轴)中,点 的极坐标为(4,
的极坐标为(4,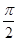 ),判断点
),判断点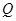 是曲线
是曲线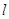 经过点
经过点 ,倾斜角
,倾斜角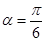 ,
,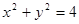 相交于
相交于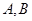 两点,求点
两点,求点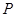 到
到
 (
( 为参数)和直线
为参数)和直线 (其中为参数,
(其中为参数, 为直线的倾斜角),如果直线与圆
为直线的倾斜角),如果直线与圆 有公共点,求
有公共点,求