题目内容
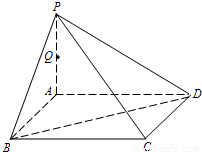
如图,P是正方形ABCD的对角线BD上的任意一点,PECF是矩形,用向量证明PA=EF且PA⊥EF.
思路分析:把几何图形放在适当的坐标系中,赋予有关点与向量具体的坐标,进行相应的代数运算和向量运算.
证明:以点D为坐标原点,DC所在直线为x轴,建立如右图所示的坐标系,设正方形边长为1.又设P(λ,λ)(0<λ<1),则A(0,1),E(λ,0),F(1,λ),
∴|![]() |=
|=![]() ,
,
|![]() |=
|=![]() (1-λ)2+λ2=2λ2-2λ+1.
(1-λ)2+λ2=2λ2-2λ+1.
∴|![]() |=|
|=|![]() |,即PA=EF.
|,即PA=EF.
由![]() ·
·![]() =(-λ,1-λ)·(1-λ,λ)=(-λ)×(1-λ)+(1-λ)·λ
=(-λ,1-λ)·(1-λ,λ)=(-λ)×(1-λ)+(1-λ)·λ
=-λ+λ2+λ-λ2=0.
∴![]() ⊥
⊥![]() ,即PA⊥EF.
,即PA⊥EF.


练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
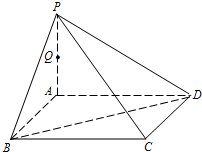 如图,P是正方形ABCD所在平面外一点,PA⊥AB,PA⊥AD,点Q是PA的中点,PA=4,AB=2.
如图,P是正方形ABCD所在平面外一点,PA⊥AB,PA⊥AD,点Q是PA的中点,PA=4,AB=2.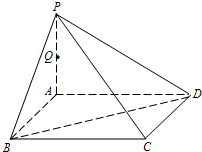 如图,P是正方形ABCD所在平面外一点,PA⊥AB,PA⊥AD,点Q是PA的中点,PA=4,AB=2.
如图,P是正方形ABCD所在平面外一点,PA⊥AB,PA⊥AD,点Q是PA的中点,PA=4,AB=2.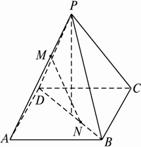
 如图,P是正方形ABCD所在平面外一点,PA⊥AB,PA⊥AD,点Q是PA的中点,PA=4,AB=2.
如图,P是正方形ABCD所在平面外一点,PA⊥AB,PA⊥AD,点Q是PA的中点,PA=4,AB=2.