题目内容
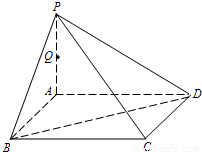
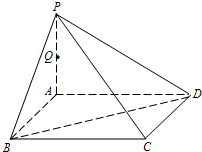 如图,P是正方形ABCD所在平面外一点,PA⊥AB,PA⊥AD,点Q是PA的中点,PA=4,AB=2.
如图,P是正方形ABCD所在平面外一点,PA⊥AB,PA⊥AD,点Q是PA的中点,PA=4,AB=2.(1)求证:PC⊥BD;
(2)求点Q到BD的距离;
(3)求点A到平面QBD的距离.
分析:(1)先证明PA⊥平面ABCD,由于AC为斜线PC在平面ABCD内的射影,AC⊥BD,根据三垂线定理可证PC⊥BD;
(2)设AC∩BD=O,连接OQ,则可知OQ的长就是点Q到BD的距离,从而可求点Q到BD的距离;
(3)过A作AH⊥OQ于H,则可知AH的长就是点A到平面QBD的距离,在△QAO中,利用等面积可求.
(2)设AC∩BD=O,连接OQ,则可知OQ的长就是点Q到BD的距离,从而可求点Q到BD的距离;
(3)过A作AH⊥OQ于H,则可知AH的长就是点A到平面QBD的距离,在△QAO中,利用等面积可求.
解答:解:(1) 连接AC
连接AC
∵PA⊥AB,PA⊥AD,AB∩AD=A
∴PA⊥平面ABCD(2分)
∴AC为斜线PC在平面ABCD内的射影
∵ABCD是正方形
∴AC⊥BD
∴PC⊥BD(4分)
(2)设AC∩BD=O,连接OQ
∵Q为PA中点,O为AC中点
∴OQ∥PC
∵PC⊥BD
∴OQ⊥BD
∴OQ的长就是点Q到BD的距离(7分)
∵AB=2,PA=4∴AC=2
∴OA=
,QA=2
∴OQ=
=
即点Q到BD的距离为
(9分)
(3)过A作AH⊥OQ于H
∵BD⊥QO,BD⊥PA
∴BD⊥平面AOQ∴BD⊥AH
又AH⊥OQ
∴AH⊥平面QBD
∴AH的长就是点A到平面QBD的距离(12分)
在△QAO中,OQ=
,AQ=2,AO=
∴AH=
=
=
(14分)
 连接AC
连接AC∵PA⊥AB,PA⊥AD,AB∩AD=A
∴PA⊥平面ABCD(2分)
∴AC为斜线PC在平面ABCD内的射影
∵ABCD是正方形
∴AC⊥BD
∴PC⊥BD(4分)
(2)设AC∩BD=O,连接OQ
∵Q为PA中点,O为AC中点
∴OQ∥PC
∵PC⊥BD
∴OQ⊥BD
∴OQ的长就是点Q到BD的距离(7分)
∵AB=2,PA=4∴AC=2
| 2 |
∴OA=
| 2 |
∴OQ=
| QA2+OA2 |
| 6 |
即点Q到BD的距离为
| 6 |
(3)过A作AH⊥OQ于H
∵BD⊥QO,BD⊥PA
∴BD⊥平面AOQ∴BD⊥AH
又AH⊥OQ
∴AH⊥平面QBD
∴AH的长就是点A到平面QBD的距离(12分)
在△QAO中,OQ=
| 6 |
| 2 |
∴AH=
| AQ • AO |
| OQ |
2×
| ||
|
2
| ||
| 3 |
点评:本题以线线垂直为载体,考查线面垂直,考查点线、点面距离,关键是得出表示点线、点面距离的线段.

练习册系列答案
相关题目
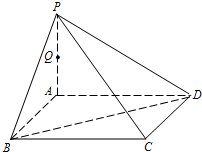 如图,P是正方形ABCD所在平面外一点,PA⊥AB,PA⊥AD,点Q是PA的中点,PA=4,AB=2.
如图,P是正方形ABCD所在平面外一点,PA⊥AB,PA⊥AD,点Q是PA的中点,PA=4,AB=2.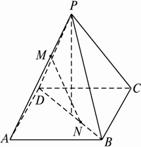
 如图,P是正方形ABCD所在平面外一点,PA⊥AB,PA⊥AD,点Q是PA的中点,PA=4,AB=2.
如图,P是正方形ABCD所在平面外一点,PA⊥AB,PA⊥AD,点Q是PA的中点,PA=4,AB=2.