题目内容
请仔细阅读以下材料:
已知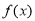 是定义在
是定义在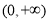 上的单调递增函数.
上的单调递增函数.
求证:命题“设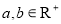 ,若
,若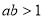 ,则
,则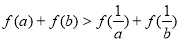 ”是真命题.
”是真命题.
证明:因为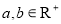 ,由
,由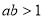 得
得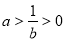 .
.
又因为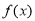 是定义在
是定义在 上的单调递增函数,
上的单调递增函数,
于是有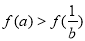 . ①
. ①
同理有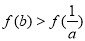 . ②
. ②
由① + ②得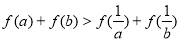 .
.
故,命题“设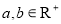 ,若
,若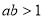 ,则
,则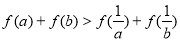 ”是真命题.
”是真命题.
请针对以上阅读材料中的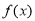 ,解答以下问题:
,解答以下问题:
(1)试用命题的等价性证明:“设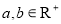 ,若
,若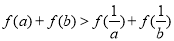 ,则:
,则: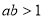 ”是真命题;
”是真命题;
(2)解关于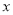 的不等式
的不等式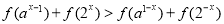 (其中
(其中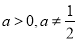 ).
).
(1)证明见解析;(2)①当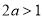 时,即
时,即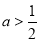 时,不等式的解集为:
时,不等式的解集为: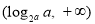
②当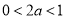 时,即
时,即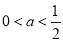 时,不等式的解集为:
时,不等式的解集为: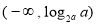
【解析】
试题分析:(1)在判断四种命题的关系时,首先要分清命题的条件和结论,当确定了原命题时,要能根据四种命题的关系写出其他三种命题;(2)当一个命题有大前提时,若要写出其他三种命题,大前提需保持不变;(3)判断一个命题为真命题,要给出推理证明;说明一个命题是假命题,只需举出反例;(4)根据“原命题与逆否命题同真同假,逆命题与否命题同真同假”这一性质,当一个命题直接判断不易进行时,可转化为判断其等价命题的真假.
试题解析: 【解析】
(1)原命题与原命题的逆否命题是等价命题.
原命题的逆否命题:设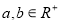 ,若
,若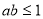 ,则:
,则: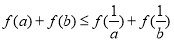 4分
4分
下面证明原命题的逆否命题为真命题:
因为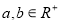 ,由
,由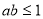 得:
得: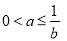 , 1分
, 1分
又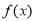 是定义在
是定义在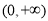 上的单调递增函数
上的单调递增函数
所以 (1) 1分
(1) 1分
同理有: (2) 1分
(2) 1分
由(1)+(2)得: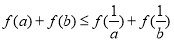 1分
1分
所以原命题的逆否命题为真命题
所以原命题为真命题. 1分
(2)由(1)的结论有: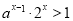 ,即:
,即: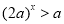 3分
3分
①当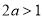 时,即
时,即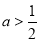 时,不等式的解集为:
时,不等式的解集为: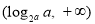 3分
3分
②当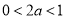 时,即
时,即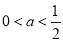 时,不等式的解集为:
时,不等式的解集为: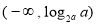 3分
3分
考点:1、命题及其相互关系;2、指数函数和对数函数的性质.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 经过点
经过点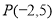 ,且斜率为
,且斜率为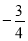 .
.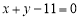 上的圆的方程.
上的圆的方程. +
+ 是必然事件 C.
是必然事件 C.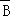 一定互斥 D.
一定互斥 D.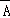 与
与 B.
B.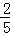 C.
C. D.
D.
 在区间
在区间 上恒成立,则实数
上恒成立,则实数 的取值范围为 .
的取值范围为 . (
( 是虚数单位)是纯虚数,则实数
是虚数单位)是纯虚数,则实数 .
. 满足以下条件:①定义在正实数集上;②
满足以下条件:①定义在正实数集上;②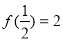 ;③对任意实数
;③对任意实数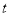 ,都有
,都有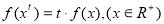 。
。 ,
,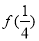 的值;
的值;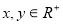 ,都有
,都有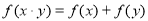 ;
;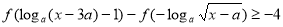 ,对
,对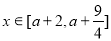 恒成立,求实数
恒成立,求实数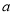 的取值范围。
的取值范围。 B.
B.  C.
C.  D.
D. 