题目内容
已知：F1和F2为双曲线
-
=1（a＞0，b＞0）的两个焦点，F1，F2，P（0，2b）是正三角形的三个顶点，
（1）求：双曲线的离心率；
（2）若双曲线经过点Q（4，6），求：双曲线的方程．
| x2 |
| a2 |
| y2 |
| b2 |
（1）求：双曲线的离心率；
（2）若双曲线经过点Q（4，6），求：双曲线的方程．
（1）∵F1，F2，P（0，2b）构成正三角形，∴2b=
c，
即有3c2=4（c2-a2），则e=
=2；
（2）∵双曲线
-
=1（a＞0，b＞0）的离心率e=
=2，∴c2=4a2，
∵c2=a2+b，∴b2=3a2，∴双曲线方程变为
-
=1，
∵双曲线经过点Q（4，6），∴
-
=1，
∴a2=4，则双曲线方程为
-
=1．
| 3 |
即有3c2=4（c2-a2），则e=
| c |
| a |
（2）∵双曲线
| x2 |
| a2 |
| y2 |
| b2 |
| c |
| a |
∵c2=a2+b，∴b2=3a2，∴双曲线方程变为
| x2 |
| a2 |
| y2 |
| 3a2 |
∵双曲线经过点Q（4，6），∴
| 16 |
| a2 |
| 36 |
| 3a2 |
∴a2=4，则双曲线方程为
| x2 |
| 4 |
| y2 |
| 12 |
练习册系列答案
开心口算题卡系列答案
口算题卡河北少年儿童出版社系列答案
A加金题 系列答案
相关题目
-
=1（a＞0，b＞0）的两个焦点，F1，F2，P（0，2b）是正三角形的三个顶点，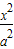
-
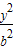=1（a＞0，b＞0）的两个焦点，F1，F2，P（0，2b）是正三角形的三个顶点，