题目内容
已知:F1和F2为双曲线 -
- =1(a>0,b>0)的两个焦点,F1,F2,P(0,2b)是正三角形的三个顶点,
=1(a>0,b>0)的两个焦点,F1,F2,P(0,2b)是正三角形的三个顶点,
(1)求:双曲线的离心率;
(2)若双曲线经过点Q(4,6),求:双曲线的方程.
解:(1)∵F1,F2,P(0,2b)构成正三角形,∴ ,
,
即有3c2=4(c2-a2),则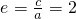 ;
;
(2)∵双曲线 (a>0,b>0)的离心率
(a>0,b>0)的离心率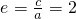 ,∴c2=4a2,
,∴c2=4a2,
∵c2=a2+b,∴b2=3a2,∴双曲线方程变为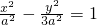 ,
,
∵双曲线经过点Q(4,6),∴ ,
,
∴a2=4,则双曲线方程为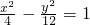 .
.
分析:(1)利用F1,F2,P(0,2b)构成正三角形,可得几何量之间的关系,即可求双曲线的离心率;
(2)利用离心率化简双曲线的方程,代入点的坐标,即可求得双曲线的方程.
点评:本题考查双曲线的标准方程与几何性质,考查学生的计算能力,属于基础题.
 ,
,即有3c2=4(c2-a2),则
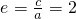 ;
;(2)∵双曲线
 (a>0,b>0)的离心率
(a>0,b>0)的离心率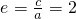 ,∴c2=4a2,
,∴c2=4a2,∵c2=a2+b,∴b2=3a2,∴双曲线方程变为
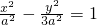 ,
,∵双曲线经过点Q(4,6),∴
 ,
,∴a2=4,则双曲线方程为
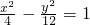 .
.分析:(1)利用F1,F2,P(0,2b)构成正三角形,可得几何量之间的关系,即可求双曲线的离心率;
(2)利用离心率化简双曲线的方程,代入点的坐标,即可求得双曲线的方程.
点评:本题考查双曲线的标准方程与几何性质,考查学生的计算能力,属于基础题.

练习册系列答案
相关题目
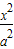 -
-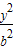 =1(a>0,b>0)的两个焦点,F1,F2,P(0,2b)是正三角形的三个顶点,
=1(a>0,b>0)的两个焦点,F1,F2,P(0,2b)是正三角形的三个顶点,