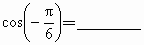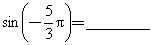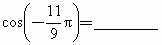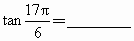题目内容
| 1-cos210° |
| 1+cos210° |
分析：把210°变为180°+30°后，利用诱导公式及特殊角的三角函数值化简，即可得到原式的值．
解答：解：原式=
+
=
+
=
+
=|sin30°+cos30°|+|sin30°-cos30°|
=
+
+
-
=
．
故答案为：
| 1-cos(180°+30°) |
| 1+cos(180°+30°) |
=
| 1+cos30° |
| 1-cos30° |
=
| 1+sin60° |
| 1-sin60° |
=|sin30°+cos30°|+|sin30°-cos30°|
=
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
| 1 |
| 2 |
=
| 3 |
故答案为：
| 3 |
点评：此题考查学生灵活运用诱导公式及特殊角的三角函数值化简求值，是一道综合题．
练习册系列答案
相关题目
将下列三角函数转化为锐角三角函数，并填在题中横线上：
|
(1)cos210° ＝________； |
(2)sin263°42′ ＝________； |
|
(3) |
(4) |
|
(5) |
(6)cos( －104°26′)＝________； |
|
(7)tan632°24′ ＝________； |
(8) |
）；(2)tan(-855°)；(3)cos210°.
）；(2)tan(-855°)；(3)cos210°.