题目内容
若θ是钝角,则满足等式log2(x2-x+2)=sinθ-
cosθ的实数x的取值范围是( )
| 3 |
| A.(-1,2) | B.(-1,0)∪(1,2) | C.[0,1] | D.[-1,0)∪(1,2] |
因为sinθ-
cosθ=2sin(θ-
),θ是钝角,
∴θ-
∈(
,
),2sin(θ-
)∈(1,2]
log2(x2-x+2)=sinθ-
cosθ,可得,
2<x2-x+2≤4,
解2<x2-x+2得x∈(-∞,0)∪(1,+∞).
解x2-x+2≤4,解得x∈[-1,2].
所以所求x的范围是:[-1,0)∪(1,2],
故选D.
| 3 |
| π |
| 3 |
∴θ-
| π |
| 3 |
| π |
| 6 |
| 2π |
| 3 |
| π |
| 3 |
log2(x2-x+2)=sinθ-
| 3 |
2<x2-x+2≤4,
解2<x2-x+2得x∈(-∞,0)∪(1,+∞).
解x2-x+2≤4,解得x∈[-1,2].
所以所求x的范围是:[-1,0)∪(1,2],
故选D.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
若O是△ABC所在平面内的一点,且向量
,
,
满足条件
+
=-
,|
|=|
|=|
|,则△ABC的形状是( )
| OA |
| OB |
| OC |
| OA |
| OB |
| OC |
| OA |
| OB |
| OC |
| A、钝角三角形 |
| B、锐角三角形 |
| C、直角三角形 |
| D、等边三角形 |
 内有一点
内有一点 ,满足
,满足 ,且
,且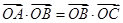 ,则
,则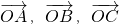 满足条件
满足条件 ,
, ,则△ABC的形状是
,则△ABC的形状是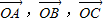 满足条件
满足条件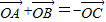 ,
,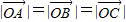 ,则△ABC的形状是( )
,则△ABC的形状是( )