题目内容
【题目】已知![]() 的内角
的内角![]() ,
,![]() ,
,![]() 的对边分别为
的对边分别为![]() ,
,![]() ,
,![]() ,且满足
,且满足![]() .
.
(Ⅰ)求角![]() ;
;
(Ⅱ)向量![]() ,
,![]() ,若函数
,若函数![]() 的图象关于直线
的图象关于直线![]() 对称,求角
对称,求角![]() 、
、![]() .
.
【答案】(I)![]() ;(II)
;(II)![]() .
.
【解析】试题分析:
(I)根据同角的基本关系可知![]() , 再由正弦定理和余弦定理即可求出
, 再由正弦定理和余弦定理即可求出![]() ,再根据
,再根据![]() ,即可求出角
,即可求出角![]() 的值;(II)解法一:根据数量积公式和恒等变换可知
的值;(II)解法一:根据数量积公式和恒等变换可知![]() ,其中
,其中![]() ,所以
,所以![]() 的图象关于直线
的图象关于直线![]() 对称,可得
对称,可得![]() ,在根据
,在根据![]() ,即
,即![]() ,在由(I)得
,在由(I)得![]() ,可得
,可得![]() ,由此即可求出结果.
,由此即可求出结果.
解法二:同方法一,可得![]() ,
,![]() 的图象关于直线
的图象关于直线![]() 对称,可得
对称,可得![]() ,即
,即![]() , 然后再同方法一即可求出结果.
, 然后再同方法一即可求出结果.
试题解析:
(I)由已知得:![]() ,
,
由正弦定理得:![]() ,
,
由余弦定理可得![]() .
.
![]() ,
,![]() .
.
(II)解法一:![]() ,
,
其中![]() ,
,
∵![]() 的图象关于直线
的图象关于直线![]() 对称,∴
对称,∴![]() ,
,
∴![]() ,
,
∴![]() ,即
,即![]() ,
,
由(I)得![]() ,
,
∴![]() ,解得
,解得![]() ,
,
∴![]() .
.
解法二:![]() ,
,
∵![]() 的图象关于直线
的图象关于直线![]() 对称,∴
对称,∴![]() ,
,
即![]() ,
,
由(I)得![]() ,∴
,∴![]() ,
,
解得![]() ,
,
∴![]() .
.

 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案【题目】计划在某水库建一座至多安装![]() 台发电机的水电站,过去
台发电机的水电站,过去![]() 年的水文资料显示,水库年入流量
年的水文资料显示,水库年入流量![]() (年入流量:一年内上游来水与库区降水之和.单位:亿立方米)都在40以上,不足
(年入流量:一年内上游来水与库区降水之和.单位:亿立方米)都在40以上,不足![]() 的年份有
的年份有![]() 年,不低于
年,不低于![]() 且不超过
且不超过![]() 的年份有
的年份有![]() 年,超过
年,超过![]() 的年份有
的年份有![]() 年,将年入流量在以上三段的频率作为相应段的概率,假设各年的年入流量相互独立.
年,将年入流量在以上三段的频率作为相应段的概率,假设各年的年入流量相互独立.
(1)求未来![]() 年中,设
年中,设![]() 表示流量超过
表示流量超过![]() 的年数,求
的年数,求![]() 的分布列及期望;
的分布列及期望;
(2)水电站希望安装的发电机尽可能运行,但每年发电机最多可运行台数受年入流量![]() 限制,并有如下关系:
限制,并有如下关系:
年入流量 |
|
|
|
发电机最多可运行台数 |
|
|
|
若某台发电机运行,则该台年利润为![]() 万元,若某台发电机未运行,则该台年亏损
万元,若某台发电机未运行,则该台年亏损![]() 万元,欲使水电站年总利润的均值达到最大,应安装发电机多少台?
万元,欲使水电站年总利润的均值达到最大,应安装发电机多少台?
【题目】为了监控某种零件的一条生产线的生产过程,检验员每天从该生产线上随机抽取16个零件,并测量其尺寸(单位:cm).根据长期生产经验,可以认为这条生产线正常状态下生产的零件的尺寸服从正态分布![]() .
.
(1)假设生产状态正常,记X表示一天内抽取的16个零件中其尺寸在![]()
之外的零件数,求![]() ;
;
(2)一天内抽检零件中,如果出现了尺寸在![]() 之外的零件,就认为这条生产线在这一天的生产过程可能出现了异常情况,需对当天的生产过程进行检查.
之外的零件,就认为这条生产线在这一天的生产过程可能出现了异常情况,需对当天的生产过程进行检查.
下面是检验员在一天内抽取的16个零件的尺寸:
9.95 | 10.12 | 9.96 | 9.96 | 10.01 | 9.92 | 9.98 | 10.04 |
10.26 | 9.91 | 10.13 | 10.02 | 9.22 | 10.04 | 10.05 | 9.95 |
经计算得![]() ,
, 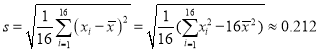 ,其中
,其中![]() 为抽取的第
为抽取的第![]() 个零件的尺寸,
个零件的尺寸, ![]() .
.
用样本平均数![]() 作为
作为![]() 的估计值
的估计值![]() ,用样本标准差
,用样本标准差![]() 作为
作为![]() 的估计值
的估计值![]() ,利用估计值判断是否需对当天的生产过程进行检查?剔除
,利用估计值判断是否需对当天的生产过程进行检查?剔除![]() 之外的数据,用剩下的数据估计
之外的数据,用剩下的数据估计![]() 和
和![]() (精确到0.01).
(精确到0.01).
附:若随机变量![]() 服从正态分布
服从正态分布![]() ,则
,则![]() ,
,
![]() ,
, ![]() .
.