ΧβΡΩΡΎ»ί
ΓΨΧβΡΩΓΩ»γΆΦΘ§ΥΡ±Ώ–Έ![]() «Ρ≥ –÷––Ρ“Μ±Ώ≥ΛΈΣ
«Ρ≥ –÷––Ρ“Μ±Ώ≥ΛΈΣ![]() ΑΌΟΉΒΡ’ΐΖΫ–ΈΒΊΩιΒΡΤΫΟφ Ψ“βΆΦ. œ÷ΦΤΜ°‘ΎΗΟΒΊΩι…œΜ°Ζ÷ΥΡΗωΆξ»ΪœύΆ§ΒΡ÷±Ϋ«»ΐΫ«–ΈΘ®Φ¥
ΑΌΟΉΒΡ’ΐΖΫ–ΈΒΊΩιΒΡΤΫΟφ Ψ“βΆΦ. œ÷ΦΤΜ°‘ΎΗΟΒΊΩι…œΜ°Ζ÷ΥΡΗωΆξ»ΪœύΆ§ΒΡ÷±Ϋ«»ΐΫ«–ΈΘ®Φ¥![]() ΚΆ
ΚΆ![]() Θ©Θ§«“‘Ύ’βΥΡΗω÷±Ϋ«»ΐΫ«–Έ«χ”ρΡΎΫχ––¬ΧΜ·Θ§÷–ΦδΒΡ–Γ’ΐΖΫ–Έ–όΫ®≥… –ΟώΫΓ…μΙψ≥ΓΘ§ΈΣΝΥΖΫ±ψ –ΟώΒΫ¥οΫΓ…μΙψ≥ΓΘ§Ρβ–όΫ®
Θ©Θ§«“‘Ύ’βΥΡΗω÷±Ϋ«»ΐΫ«–Έ«χ”ρΡΎΫχ––¬ΧΜ·Θ§÷–ΦδΒΡ–Γ’ΐΖΫ–Έ–όΫ®≥… –ΟώΫΓ…μΙψ≥ΓΘ§ΈΣΝΥΖΫ±ψ –ΟώΒΫ¥οΫΓ…μΙψ≥ΓΘ§Ρβ–όΫ®![]() Χθ¬Ζ
Χθ¬Ζ![]()
![]()
![]()
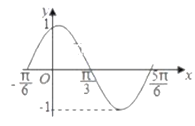
![]() . “―÷Σ‘Ύ÷±Ϋ«»ΐΫ«–ΈΡΎΫχ––¬ΧΜ·ΟΩ1ΆρΤΫΖΫΟΉΒΡΖ―”ΟΈΣ
. “―÷Σ‘Ύ÷±Ϋ«»ΐΫ«–ΈΡΎΫχ––¬ΧΜ·ΟΩ1ΆρΤΫΖΫΟΉΒΡΖ―”ΟΈΣ![]() ‘ΣΘ§÷–Φδ–Γ’ΐΖΫ–Έ–όΫ®Ιψ≥ΓΟΩ1ΆρΤΫΖΫΟΉΒΡΖ―”ΟΈΣ
‘ΣΘ§÷–Φδ–Γ’ΐΖΫ–Έ–όΫ®Ιψ≥ΓΟΩ1ΆρΤΫΖΫΟΉΒΡΖ―”ΟΈΣ![]() ‘ΣΘ§–ό¬ΖΟΩ1ΑΌΟΉΒΡΖ―”ΟΈΣ
‘ΣΘ§–ό¬ΖΟΩ1ΑΌΟΉΒΡΖ―”ΟΈΣ![]() ‘ΣΘ§Τδ÷–
‘ΣΘ§Τδ÷–![]() ΈΣ’ΐ≥Θ ΐΘ°…η
ΈΣ’ΐ≥Θ ΐΘ°…η![]() Θ§
Θ§![]() .
.
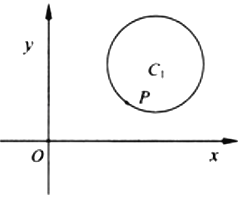
Θ®1Θ©”Ο![]() ±μ ΨΗΟΙΛ≥ΧΒΡΉή‘λΦέ
±μ ΨΗΟΙΛ≥ΧΒΡΉή‘λΦέ![]() ΘΜ
ΘΜ
Θ®2Θ©Β±![]() ΈΣΚΈ÷Β ±Θ§ΗΟΙΛ≥ΧΒΡΉή‘λΦέΉνΒΆΘΩ
ΈΣΚΈ÷Β ±Θ§ΗΟΙΛ≥ΧΒΡΉή‘λΦέΉνΒΆΘΩ
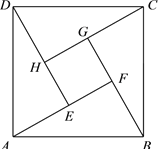
ΓΨ¥πΑΗΓΩΘ®1Θ©![]() Θ§
Θ§![]() ΘΜΘ®2Θ©Β±
ΘΜΘ®2Θ©Β±![]() ±Θ§
±Θ§![]() »ΓΒΟΉν–Γ÷Β
»ΓΒΟΉν–Γ÷Β
ΓΨΫβΈωΓΩ
(1)ΗυΨίΧβ“βΩ…÷Σ![]() ,
,![]() ,ΫχΕχ«σΒΟ
,ΫχΕχ«σΒΟ![]() ”κ
”κ![]() ‘Ό«σΒΟΉή‘λΦέ
‘Ό«σΒΟΉή‘λΦέ![]() Φ¥Ω….
Φ¥Ω….
(2)”…(1)”–![]() ,‘Ό«σΒΦΖ÷ΈωΚ· ΐΒΡΒΞΒς–‘”κΉν÷ΒΦ¥Ω….
,‘Ό«σΒΦΖ÷ΈωΚ· ΐΒΡΒΞΒς–‘”κΉν÷ΒΦ¥Ω….
Θ®1Θ©‘Ύ![]() ÷–,
÷–,![]() ,
,![]() ,Υυ“‘
,Υυ“‘![]() ,
,![]() .
.
”…”Ύ![]() ΚΆ
ΚΆ![]() «ΥΡΗωΆξ»ΪœύΆ§ΒΡ÷±Ϋ«»ΐΫ«–Έ,Υυ“‘
«ΥΡΗωΆξ»ΪœύΆ§ΒΡ÷±Ϋ«»ΐΫ«–Έ,Υυ“‘![]() ,
,![]() ,
,
Υυ“‘![]() ,
,
![]() .
.
Υυ“‘![]()
![]()
![]() ,
,![]() .
.
Θ®2Θ©”…Θ®1Θ©Φ«![]() ,
,![]() .
.
‘ρ![]() .
.
Νν![]() ,“ρΈΣ
,“ρΈΣ![]() ,Υυ“‘
,Υυ“‘![]() Μρ
Μρ![]() (…α).
(…α).
Φ«![]() ,Υυ“‘Β±
,Υυ“‘Β±![]() ±,
±,![]() ,
,![]() ΒΞΒςΒίΦθΘΜ
ΒΞΒςΒίΦθΘΜ
Β±![]() ±,
±,![]() ,
,![]() ΒΞΒςΒί‘ω. Υυ“‘Β±
ΒΞΒςΒί‘ω. Υυ“‘Β±![]() ±,
±,![]() »ΓΒΟΦΪ–Γ÷Β,“≤ «Ήν–Γ÷Β,
»ΓΒΟΦΪ–Γ÷Β,“≤ «Ήν–Γ÷Β,
”÷![]() ,Υυ“‘Β±
,Υυ“‘Β±![]() ±,
±,![]() »ΓΒΟΉν–Γ÷Β.
»ΓΒΟΉν–Γ÷Β.

 Ωλά÷–Γ≤© ΩΙ°ΙΧ”κΧαΗΏœΒΝ–¥πΑΗ
Ωλά÷–Γ≤© ΩΙ°ΙΧ”κΧαΗΏœΒΝ–¥πΑΗ