题目内容
1.已知函数f(x)=(x-k)ex(k∈R).(1)求f(x)的单调区间和极值;
(2)求f(x)在x∈[1,2]上的最小值;
(3)设g(x)=f(x)+f′(x),若对${?^{\;}}^{\;}k∈[{\frac{3}{2},\frac{5}{2}}]$及?x∈[0,1]有g(x)≥λ恒成立,求实数λ的取值范围.
分析 (1)由f(x)=(x-k)ex,求导f′(x)=(x-k+1)ex,令f′(x)=0,求得x=k-1,令f′(x)<0,解得函数的单调递减区间,f′(x)>0,解得函数的单调递增区间,根据函数的单调性即可求得f(x)的极值;
(2)当k-1≤1时,f(x)在[1,2]单调递增,f(x)的最小值为f(1),当k-1≥2时,f(x)在[1,2]单调递减,f(x)的最小值为f(2),当1<k-1<2时,则x=k-1时,f(x)取最小值,最小值为:-ek-1;
(3)由g(x)=(2x-2k+1)ex,求导g′(x)=(2x-2k+3)ex,当g′(x)<0,解得:x<k-$\frac{3}{2}$,求得函数的单调递减区间,当g′(x)>0,解得:x>k-$\frac{3}{2}$,求得函数的单调递增区间,由题意可知g(x)≥λ,?x∈[0,1]恒成立,等价于g(k-$\frac{3}{2}$)=-2e${\;}^{k-\frac{3}{2}}$≥λ,由-2e${\;}^{k-\frac{3}{2}}$≥λ,对?k∈[$\frac{3}{2}$,$\frac{5}{2}$]恒成立,根据函数的单调性,即可求得实数λ的取值范围.
解答 解:(1)f(x)=(x-k)ex(k∈R),求导f′(x)=(x-k)ex+ex=(x-k+1)ex,
令f′(x)=0,解得:x=k-1,
当x<k-1时,f′(x)<0,
当x>k-1时,f′(x)>0,
| x | (-∞,k-1) | k-1 | (k-1,+∞) |
| f′(x) | - | 0 | + |
| f(x) | ↓ | -e-k-1 | ↑ |
(2)当k-1≤1时,即k≤2时,f(x)在[1,2]单调递增,
f(x)的最小值为f(1)=(1-k)e;
当k-1≥2时,即k≥3时,f(x)在[1,2]单调递减,
∴当x=2时,f(x)的最小值为f(2)=(2-k)e3;
当1<k-1<2时,解得:2<k<3时,
∴f(x)在[1,k-1]单调递减,在[k-1,2]单调递增,
∴当x=k-1时,f(x)取最小值,最小值为:-ek-1;
(3)g(x)=f(x)+f'(x)=(x-k)ex+(x-k+1)ex=(2x-2k+1)ex,
求导g′(x)=(2x-2k+1)ex+2ex=(2x-2k+3)ex,
令g′(0)=0,2x-2k+3=0,x=k-$\frac{3}{2}$,
当x<k-$\frac{3}{2}$时,g′(x)<0,
当x>k-$\frac{3}{2}$时,g′(x)>0,
∴g(x)在(-∞,k-$\frac{3}{2}$)单调递减,在(k-$\frac{3}{2}$,+∞)单调递增,
故当x=k-$\frac{3}{2}$,g(x)取最小值,最小值为:g(k-$\frac{3}{2}$)=-2e${\;}^{k-\frac{3}{2}}$,
∵k∈[$\frac{3}{2}$,$\frac{5}{2}$],即k-$\frac{3}{2}$∈[0,1],
∴?x∈[0,1],g(x)的最小值,g(k-$\frac{3}{2}$)=-2e${\;}^{k-\frac{3}{2}}$,
∴g(x)≥λ,?x∈[0,1]恒成立,等价于g(k-$\frac{3}{2}$)=-2e${\;}^{k-\frac{3}{2}}$≥λ,
由-2e${\;}^{k-\frac{3}{2}}$≥λ,对?k∈[$\frac{3}{2}$,$\frac{5}{2}$]恒成立,
∴λ≤(-2e${\;}^{k-\frac{3}{2}}$)最小值,
令h(k)=-2e${\;}^{k-\frac{3}{2}}$,k∈[$\frac{3}{2}$,$\frac{5}{2}$],
由指数函数的性质,函数h(k)在k∈[$\frac{3}{2}$,$\frac{5}{2}$]单调递增,
∴当k=$\frac{5}{2}$时,h(k)取最小值,h($\frac{5}{2}$)=-2e,
∴λ≤-2e.
∴实数λ的取值范围(-∞,-2e).
点评 本题考查利用到时研究函数的单调性和在闭区间上的最值,考查函数导数的运算,考查转化思想,考查计算能力,属于难题.

练习册系列答案
相关题目
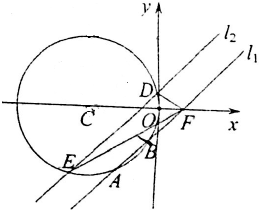 已知直线l1:y=x-1与圆C:(x+a)2+y2=a2(a>0)相交于A、B两点,|AB|=2,直线l2∥l1,直线l2与圆C相交于D、E两点.
已知直线l1:y=x-1与圆C:(x+a)2+y2=a2(a>0)相交于A、B两点,|AB|=2,直线l2∥l1,直线l2与圆C相交于D、E两点.