题目内容
16.已知函数f(x)=-x3+3x2+9x+m在区间[-2,2]上的最大值是20,则实数m的值等于-2.分析 先将f(x)的各极值与其端点的函数值比较,其中最大的一个就是最大值,最小的一个就是最小值,再根据条件求出m的值,最小值即可求得.
解答 解:∵f(x)=-x3+3x2+9x+m(m为常数)
∴f′(x)=-3x2+6x+9
令f′(x)=-3x2+6x+9=0,解得x=-1或3(舍去)
当-2<x<-1时,f'(x)<0,
当-1<x<2时,f'(x)>0
∴当x=-1时取最小值,而f(2)=22+m>f(-2)=2+m,
即最大值为22+m=20,∴m=-2,
故答案为:-2.
点评 本题主要考查了利用导数求闭区间上函数的最值,是高考中常考的知识点,解题的关键是利用导数工具,确定函数的最值,属于中档题.

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目
11.二面角α-l-β为60°,A、B是棱上的两点,AC、BD分别在半平面α、β内,AC⊥l,BD⊥l且AB=AC=1,BD=2,则CD的长为( )
| A. | 1 | B. | $\sqrt{3}$ | C. | 2 | D. | $\sqrt{5}$ |
5.定义在R上的可导函数f(x),当x∈(0,+∞)时,xf′(x)-f(x)>0恒成立,a=f(1),b=$\frac{1}{2}f(2),c=\frac{{\sqrt{2}}}{2}f({\sqrt{2}})$,则a,b,c的大小关系为( )
| A. | c<a<b | B. | b<c<a | C. | a<c<b | D. | c<b<a |
6.23000的末两位数是( )
| A. | 46 | B. | 56 | C. | 66 | D. | 76 |
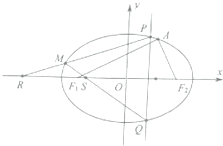 如图,已知椭圆C:$\frac{{x}^{2}}{9}+\frac{{y}^{2}}{{b}^{2}}=1(0<b<3)$的左、右焦点分别为F1、F2,椭圆上存在一点A,使得AF1=2AF2,且∠F1AF2=90°
如图,已知椭圆C:$\frac{{x}^{2}}{9}+\frac{{y}^{2}}{{b}^{2}}=1(0<b<3)$的左、右焦点分别为F1、F2,椭圆上存在一点A,使得AF1=2AF2,且∠F1AF2=90°