题目内容
11．将一枚质地均匀的硬币连续掷3次，则“出现正面的次数多于反面”的概率为（ ）| A． | $\frac{1}{2}$ | B． | $\frac{1}{3}$ | C． | $\frac{1}{4}$ | D． | $\frac{3}{8}$ |
分析 求出出现2次正面一次反面的概率，再加上3次都是正面的概率，即为所求．
解答 解：将一枚均匀的硬币投掷3次，出现2次正面一次反面的概率等于${C}_{3}^{2}$•${（\frac{1}{2}）}^{2}$•$\frac{1}{2}$=$\frac{3}{8}$，
三次都是正面的概率等于（${（\frac{1}{2}）}^{3}$=$\frac{1}{8}$，
∴掷一枚均匀的硬币3次，出现正面的次数多于反面的次数的概率是$\frac{3}{8}$+$\frac{1}{8}$=$\frac{1}{2}$，
故选：A．
点评 本题考查的知识点是古典概型概率计算公式，其中熟练掌握利用古典概型概率计算公式求概率的步骤，是解答的关键，属于基础题．
练习册系列答案
期末好成绩系列答案
99加1领先期末特训卷系列答案
百强名校期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案
金状元绩优好卷系列答案
相关题目
2．某射手有4发子弹，射击一次命中目标的概率为0.9，如果命中就停止射击，否则一直到子弹用尽，用ξ表示用的子弹数，则P（ξ=4）等于（ ）
| A． | 0.0009 | B． | 0.001 | C． | 0.009 | D． | 以上都不对 |
19．设A为圆周上一定点，在圆周上等可能地任取一点与A连结，则弦长超过半径的概率是（ ）
| A． | $\frac{1}{6}$ | B． | $\frac{1}{3}$ | C． | $\frac{1}{4}$ | D． | $\frac{2}{3}$ |
3．
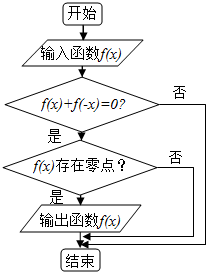某程序据图如图所示，现输入如下四个函数：f（x）=x2，f（x）=$\frac{1}{x}$，f（x）=ex，f（x）=x3，则可以输出的函数（ ）
某程序据图如图所示，现输入如下四个函数：f（x）=x2，f（x）=$\frac{1}{x}$，f（x）=ex，f（x）=x3，则可以输出的函数（ ）| A． | f（x）=x2 | B． | f（x）=$\frac{1}{x}$ | C． | f（x）=ex | D． | f（x）=x3 |
20．执行如图的程序框图，若输入n=2015，则输出T的值为（ ）
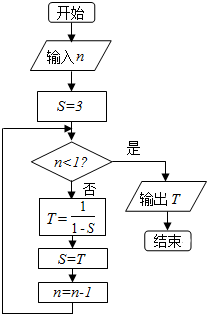
| A． | $-\frac{1}{2}$ | B． | $\frac{2}{3}$ | C． | 3 | D． | $\frac{3}{4}$ |