题目内容
3．
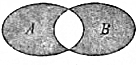如图所示的韦恩图中，A，B中两非空集合，定义集合A?B为阴影部分表示的集合，若x，y∈R，A={x|y=ln（2x-x2）}，B={y|y=ex，x＞0}，则A?B为（ ）| A． | {x|0＜x＜2} | B． | {x|x≤1或x≥2} | C． | {x|0≤x≤1或x≥2} | D． | {x|0＜x≤1或x≥2} |
分析 根据Venn图可知阴影部分的集合为{x|x∈A∪B且x∉A∩B}，根据集合的基本运算进行求解即可．
解答 解：A={x|y=ln（2x-x2）}=A={x|2x-x2＞0}={x|0＜x＜2}，
B={y|y=ex，x＞0}={y|y＞1}，
则A∪B={x|x＞0}，A∩B={x|1＜x＜2}，
则A?B={x|x∈A∪B且x∉A∩B}={x|0＜x≤1或x≥2}，
故选：D
点评 本题主要考查集合的基本运算，根据条件判断A?B={x|x∈A∪B且x∉A∩B}是解决本题的关键．
练习册系列答案
导学与测试系列答案
新非凡教辅冲刺100分系列答案
相关题目
18．设?是1的一个7次虚单位根，则有$\frac{?}{1+{?}^{2}}$+$\frac{{?}^{2}}{1+{?}^{4}}$+$\frac{{?}^{3}}{1{+?}^{6}}$=-2．
2．
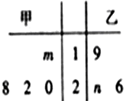已知甲、乙两组数据如茎叶图所示，若它们的中位数相同，平均数也相同，则图中的$\frac{m}{n}$=（ ）
已知甲、乙两组数据如茎叶图所示，若它们的中位数相同，平均数也相同，则图中的$\frac{m}{n}$=（ ）| A． | $\frac{1}{8}$ | B． | 8 | C． | 9 | D． | $\frac{1}{9}$ |
6．某车间为了规定工时定额，需要确定加工零件所花费的时间，为此进行了四次试验如下：
（1）求y关于x的线性回归方程
（2）试预测加工10个零件需要多少时间？
$\widehat{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{xy}}{\sum_{i=1}^{n}{x}_{i}^{2}-n{\overline{x}}^{2}}$ $\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$．
| 零件的个数x/个 | 2 | 3 | 4 | 5 |
| 加工的时间y/小时 | 2.5 | 3 | 4 | 4.5 |
（2）试预测加工10个零件需要多少时间？
$\widehat{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{xy}}{\sum_{i=1}^{n}{x}_{i}^{2}-n{\overline{x}}^{2}}$ $\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$．