题目内容
对于函数
若存在
，使
成立，则称
为的不动点。已知函数
（1）当
时，求的不动点；
（2）若对于任意实数
，函数恒有两个相异不动点，求
的取值范围
。
解：（1）
，因为为不动点，所以
解得
和3是函数的两个不动点，
（2）因为函数恒有两个相异的不动点，
所以方程
也
就是
对任何实数恒有两个不相等的实数根，
即
对任意的
恒成立，
这个不等式可化为
所以
，解得
练习册系列答案
相关题目
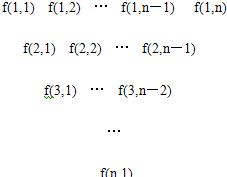一个三角形数表按如下方式构成：第一行依次写上n（n≥4）个数，在上一行的每相邻两数的中间正下方写上这两数之和，得到下一行，依此类推．记数表中第i行的第j个数为f（i，j）．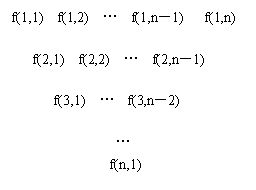
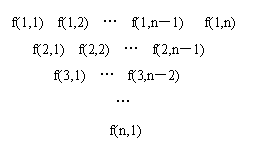，试求一个函数g(x)，使得
，且对于任意的m∈(
,
Sn=b1g(1)+b2g(2)+…+bng(n)＜，且对于任意的m∈(,)，均存在实数，使得当n＞时，都有Sn >m.
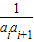，试求一个函数f（x），使得Sn=b1g（1）+b2g（2）+…+bng（n）＜
，且对于任意的m∈（
，
），均存在实数λ?，使得当n＞?λ时，都有Sn＞m．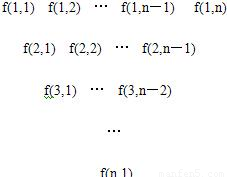
，试求一个函数f（x），使得Sn=b1g（1）+b2g（2）+…+bng（n）＜
，且对于任意的m∈（
，
），均存在实数λ?，使得当n＞?λ时，都有Sn＞m．