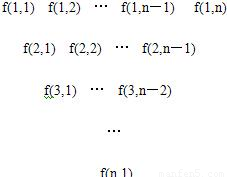题目内容
一个三角形数表按如下方式构成:第一行依次写上n(n≥4)个数,在上一行的每相邻两数的中间正下方写上这两数之和,得到下一行,依此类推.记数表中第i行的第j个数为f(i,j).
(1)若数表中第i (1≤i≤n-3)行的数依次成等差数列,求证:第i+1行的数也依次成等差数列;
(2)已知f(1,j)=4j,求f(i,1)关于i的表达式;
(3)在(2)的条件下,若f(i,1)=(i+1)(ai-1),bi= ![]() ,试求一个函数g(x),使得
,试求一个函数g(x),使得
Sn=b1g(1)+b2g(2)+…+bng(n)<![]() ,且对于任意的m∈(
,且对于任意的m∈(![]() ,
,![]() ),均存在实数l ,使得当n>l时,都有Sn >m.
),均存在实数l ,使得当n>l时,都有Sn >m.
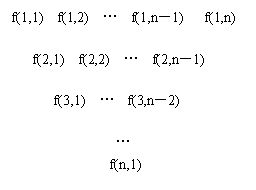
(1)数表中第![]() 行的数依次所组成数列的通项为
行的数依次所组成数列的通项为![]() ,则由题意可得
,则由题意可得
![]()
![]()
![]() (其中
(其中![]() 为第
为第![]() 行数所组成的数列的公差) (4分)
行数所组成的数列的公差) (4分)
(2)![]()
![]() 第一行的数依次成等差数列,由(1)知,第2行的数也依次成等差数列,依次类推,可知数表中任一行的数(不少于3个)都依次成等差数列。设第
第一行的数依次成等差数列,由(1)知,第2行的数也依次成等差数列,依次类推,可知数表中任一行的数(不少于3个)都依次成等差数列。设第![]() 行的数公差为
行的数公差为![]() ,则
,则![]() ,则
,则![]()
所以![]()
![]()
![]()
![]()
![]()
![]()
(3)由![]() ,可得
,可得![]()
所以![]()
![]() =
=![]()
令![]() ,则
,则![]() ,所以
,所以 ![]()
![]()
要使得![]() ,即
,即![]() ,只要
,只要![]() =
=![]() ,
,
![]() ,
,![]() ,所以只要
,所以只要![]() ,
,
即只要![]() ,所以可以令
,所以可以令![]()
则当![]() 时,都有
时,都有![]() .
.
所以适合题设的一个函数为![]()

练习册系列答案
相关题目
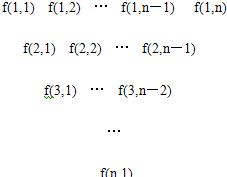 一个三角形数表按如下方式构成:第一行依次写上n(n≥4)个数,在上一行的每相邻两数的中间正下方写上这两数之和,得到下一行,依此类推.记数表中第i行的第j个数为f(i,j).
一个三角形数表按如下方式构成:第一行依次写上n(n≥4)个数,在上一行的每相邻两数的中间正下方写上这两数之和,得到下一行,依此类推.记数表中第i行的第j个数为f(i,j).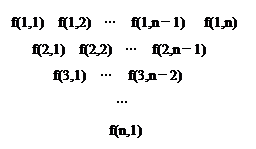
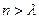 时,都有Sn >m.
时,都有Sn >m.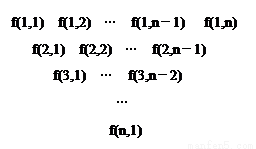 Sn=b1g(1)+b2g(2)+…+bng(n)<,且对于任意的m∈(,),均存在实数,使得当
Sn=b1g(1)+b2g(2)+…+bng(n)<,且对于任意的m∈(,),均存在实数,使得当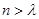 时,都有Sn >m.
时,都有Sn >m. Sn=b1g(1)+b2g(2)+…+bng(n)<,且对于任意的m∈(,),均存在实数,使得当n>时,都有Sn >m.
Sn=b1g(1)+b2g(2)+…+bng(n)<,且对于任意的m∈(,),均存在实数,使得当n>时,都有Sn >m.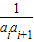 ,试求一个函数f(x),使得Sn=b1g(1)+b2g(2)+…+bng(n)<
,试求一个函数f(x),使得Sn=b1g(1)+b2g(2)+…+bng(n)< ,且对于任意的m∈(
,且对于任意的m∈( ,
, ),均存在实数λ?,使得当n>?λ时,都有Sn>m.
),均存在实数λ?,使得当n>?λ时,都有Sn>m.