题目内容
已知α、β为一个钝角三角形的两个锐角,下列四个不等式中错误的是 .①tanαtanβ<1; ②
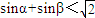 ;
;③cosα+cosβ>1; ④
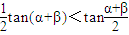 .
.
【答案】分析:可利用α+β<90°,对四个选项逐一分析.
①项中tanαtanβ<tanαtan(90°-α),②项中sinα+sinβ<sinα+sin(90°-α)=sinα+cosα,③项cosα+cosβ>cosα+cos(90°-α)通过两角和公式分析均正确.④项举α=30°,β=30°分析知结论不成立
解答:解:因为对于钝角三角形,必定有α+β<90°,所以
对于①.tanαtanβ<tanαtan(90°-α)=tanαcotα=1,故①对.
对于②.∵α+β<90°,∴0<β<90°-α<90°⇒sinβ<sin(90°-α)
∴sinα+sinβ<sinα+sin(90°-α)=sinα+cosα=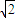 sin(α+45°)≤
sin(α+45°)≤ ,
,
即 成立;故②对.
成立;故②对.
对于③.cosα+cosβ>cosα+cos(90°-α)=cosα+sinα=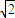 sin(α+45°)
sin(α+45°)
而0<α<90°⇒45°<α+45°<135°⇒sin(α+45°)>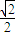 ⇒cosα+cosβ>
⇒cosα+cosβ> sin(α+45°)>1,故③对.
sin(α+45°)>1,故③对.
对于④.举个例子,假如α=30°,β=30°,则 ×tan(α+β)=
×tan(α+β)= ×tan60°=
×tan60°= ×
× =
=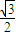 ;而tan
;而tan =tan30°=
=tan30°= 比
比 小,故等式不成立.即④不成立.
小,故等式不成立.即④不成立.
故答案为:④.
点评:本题主要考查了三角函数的恒等变换应用.要熟练掌握如角的变换法、化弦法、降幂法等常用的方法.解决本题的关键在于利用好α、β为一个钝角三角形的两个锐角这一条件.
①项中tanαtanβ<tanαtan(90°-α),②项中sinα+sinβ<sinα+sin(90°-α)=sinα+cosα,③项cosα+cosβ>cosα+cos(90°-α)通过两角和公式分析均正确.④项举α=30°,β=30°分析知结论不成立
解答:解:因为对于钝角三角形,必定有α+β<90°,所以
对于①.tanαtanβ<tanαtan(90°-α)=tanαcotα=1,故①对.
对于②.∵α+β<90°,∴0<β<90°-α<90°⇒sinβ<sin(90°-α)
∴sinα+sinβ<sinα+sin(90°-α)=sinα+cosα=
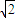 sin(α+45°)≤
sin(α+45°)≤ ,
,即
 成立;故②对.
成立;故②对.对于③.cosα+cosβ>cosα+cos(90°-α)=cosα+sinα=
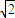 sin(α+45°)
sin(α+45°)而0<α<90°⇒45°<α+45°<135°⇒sin(α+45°)>
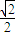 ⇒cosα+cosβ>
⇒cosα+cosβ> sin(α+45°)>1,故③对.
sin(α+45°)>1,故③对.对于④.举个例子,假如α=30°,β=30°,则
 ×tan(α+β)=
×tan(α+β)= ×tan60°=
×tan60°= ×
× =
=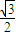 ;而tan
;而tan =tan30°=
=tan30°= 比
比 小,故等式不成立.即④不成立.
小,故等式不成立.即④不成立.故答案为:④.
点评:本题主要考查了三角函数的恒等变换应用.要熟练掌握如角的变换法、化弦法、降幂法等常用的方法.解决本题的关键在于利用好α、β为一个钝角三角形的两个锐角这一条件.

练习册系列答案
 名题金卷系列答案
名题金卷系列答案
相关题目
已知α、β为一个钝角三角形的两个锐角,下列四个不等式中错误的是( )
| A、tanαtanβ<1 | ||||
B、sinα+sinβ<
| ||||
C、
| ||||
| D、cosα+cosβ>1 |
 外接圆
外接圆 的半径为
的半径为 ,且
,且 .
. ,从圆
,从圆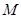 ,若点
,若点 ,判断
,判断