题目内容
已知椭圆C: ,经过点
,经过点 ,离心率
,离心率 ,直线
,直线 的方程为
的方程为  .
.
(1)求椭圆C的方程;
 (2)AB是经过右焦点F的任一弦(不经过点P),设直线l与直线AB相交于点M,记PA、PB、PM的斜率分别为
(2)AB是经过右焦点F的任一弦(不经过点P),设直线l与直线AB相交于点M,记PA、PB、PM的斜率分别为 ,问:是否存在常数
,问:是否存在常数 ,使得
,使得 ?若存在,求出
?若存在,求出 的值,若不存在,说明理由.
的值,若不存在,说明理由.
(1)由点 在
在 椭圆上得,
椭圆上得, ①
① ②
②
由 ①②得 ,故椭圆
,故椭圆 的方程为
的方程为 .......4分
.......4分
(2)假设存在常数 ,使得
,使得 .
.
由题意可设
 ③
③
代入椭圆方程 并整理得
并整理得
设 ,则有
,则有 ④......6分
④......6分
在方程③中,令 得,
得, ,从而
,从而
 .又因为
.又因为 共线,则有
共线,则有 ,
,
即有
所以


=
 ⑤
⑤
将④代入⑤得

 ,又
,又 ,
,
所以

故存在常数 符合题意......12分
符合题意......12分

练习册系列答案
 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
 次体育测试成绩的茎叶图,则甲
次体育测试成绩的茎叶图,则甲
 表示的平面区域为
表示的平面区域为 ,则区域
,则区域 的最大值为 .
的最大值为 .  与椭圆C2
与椭圆C2 B.
B. C.
C. D.
D.

 被圆
被圆 截得的弦长为4
截得的弦长为4 的最小值是
的最小值是 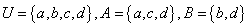 ,则
,则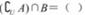
 B.
B.  C.
C.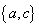 D.
D.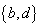
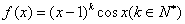 ,则( )
,则( )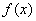 在x=1处取得极小值
在x=1处取得极小值 ,则复数
,则复数 在复平面内对应的点位于( )
在复平面内对应的点位于( ) .第一像限
.第一像限  .第二像限
.第二像限  .第三像限
.第三像限  .第四像限
.第四像限 .
. ,求函数
,求函数 在
在 处的切线方程;
处的切线方程; 时,求证:
时,求证: .
.