题目内容
已知圆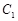 的参数方程为
的参数方程为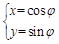 (
(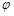 为参数),以坐标原点
为参数),以坐标原点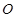 为极点,x轴的正半轴为极轴建立极坐标系,圆
为极点,x轴的正半轴为极轴建立极坐标系,圆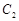 的极坐标方程为
的极坐标方程为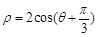 .
.
(Ⅰ)将圆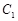 的参数方程化为普通方程,将圆
的参数方程化为普通方程,将圆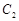 的极坐标方程化为直角坐标方程;
的极坐标方程化为直角坐标方程;
(Ⅱ)圆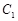 、
、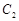 是否相交,若相交,请求出公共弦的长;若不相交,请说明理由.
是否相交,若相交,请求出公共弦的长;若不相交,请说明理由.
(Ⅰ) 。(Ⅱ)
。(Ⅱ) 。
。
解析试题分析:
思路分析:(Ⅰ)由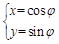 利用“平方关系”消参得到:x2+y2=1,
利用“平方关系”消参得到:x2+y2=1,
应用两角和的余弦公式变形,得到ρ=2cos(θ+ )=cosθ-
)=cosθ- sinθ,
sinθ,
即ρ2=ρcosθ- ρsinθ利用公式化为普通方程。
ρsinθ利用公式化为普通方程。
(Ⅱ)通过计算圆心距 ,
,
判断两圆相交,通过建立方程组,进一步求弦长,也可考虑“几何法”。
解:(Ⅰ)由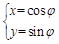 得x2+y2=1,
得x2+y2=1,
又∵ρ=2cos(θ+ )=cosθ-
)=cosθ- sinθ,
sinθ,
∴ρ2=ρcosθ- ρsinθ.∴x2+y2-x+
ρsinθ.∴x2+y2-x+ y=0,
y=0,
即 5分
5分
(Ⅱ)圆心距 ,
,
得两圆相交,由
得,A(1,0),B ,
,
∴  10分
10分
考点:极坐标方程、参数方程与普通方程的互化,参数方程的应用。
点评:中档题,参数方程化为普通方程,常用的“消参”方法有,代入消参、加减消参、平方关系消参等。利用参数方程,往往会将问题转化成三角函数问题,利用三角公式及三角函数的图象和性质,化难为易。极坐标方程化为普通方程,常用的公式有,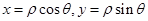 ,
, 等。
等。

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
在回归分析中,代表了数据点和它在回归直线上相应位置的差异的是( )
| A.总偏差平方和 | B.残差平方和 | C.回归平方和 | D.相关指数R2 |
 中,直线
中,直线 经过点P(0,1),曲线
经过点P(0,1),曲线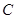 的方程为
的方程为 ,若直线
,若直线 ,
, 两点,求
两点,求 的值.
的值.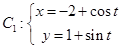 (
(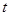 为参数),
为参数),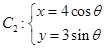 (
(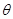 为参数).
为参数).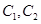 的方程为普通方程,并说明它们分别表示什么曲线;
的方程为普通方程,并说明它们分别表示什么曲线;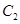 的左顶点且倾斜角为
的左顶点且倾斜角为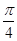 的直线
的直线 交曲线
交曲线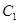 于
于 两点,求
两点,求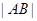 .
. ,倾斜角为
,倾斜角为 的直线
的直线 与圆C:
与圆C: (
( 为参数)相交于
为参数)相交于 两点,试确定
两点,试确定 的值.
的值. 中,曲线
中,曲线 的参数方程为
的参数方程为 (
( 为参数),若以直角坐标系的原点
为参数),若以直角坐标系的原点 为极点,
为极点, 轴的正半轴为极轴建立极坐标,曲线
轴的正半轴为极轴建立极坐标,曲线 的极坐标方程为
的极坐标方程为 (其中
(其中 为常数).
为常数). 时,求曲线
时,求曲线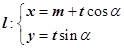 (t为参数)经过椭圆
(t为参数)经过椭圆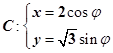 (
(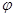 为参数)的左焦点F.
为参数)的左焦点F. 的极坐标方程为
的极坐标方程为 ,以极点为原点,极轴为轴的正半轴建立直角坐标系,直线
,以极点为原点,极轴为轴的正半轴建立直角坐标系,直线 的参数方程
的参数方程
 得到曲线
得到曲线 ,在曲线
,在曲线 上求一点
上求一点 ,使点
,使点 .
. ,求
,求 的最大值.
的最大值.