题目内容
已知曲线
的极坐标方程为
,以极点为原点,极轴为轴的正半轴建立直角坐标系,直线
的参数方程
(Ⅰ)写出直线的普通方程与曲线的直角坐标方程；
(Ⅱ)设曲线经过伸缩变换
得到曲线
,在曲线
上求一点
,使点到直线的距离最小，并求出最小距离.
（1）
，
（2）
解析试题分析：．解：（Ⅰ）由得，，
由
得，圆.
(Ⅱ)设点
是圆C上的任意一点，经过伸缩变换得到点
由得
，把代入圆得，
所以曲线
令
，则点到直线的距离
∴当
即
时，
，此时，
∴当
时，点到直线的距离的最小值为.
考点：点到直线的距离，参数方程与直角坐标方程
点评：主要是考查了参数方程与直角坐标方程的互化，以及点到直线的距离公式的求解，属于中档题。
练习册系列答案
相关题目
中，
是过定点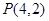
且倾斜角为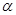
的直线；在极坐标系（以坐标原点
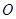为极点，以
轴非负半轴为极轴，取相同单位长度）中，曲线
的极坐标方程为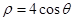
.
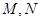，求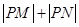
的取值范围．
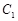的参数方程为
（
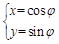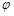为参数），以坐标原点
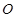为极点，x轴的正半轴为极轴建立极坐标系，圆
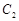的极坐标方程为
．
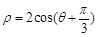有相同的长度单位，以原点
为极点，以
轴正半轴为极轴.已知直线
的参数方程为
（
为参数），曲线
的极坐标方程为
.
两点，求弦长
.
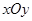中，求过椭圆
（
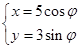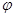为参数）的右焦点且与直线
（
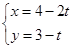为参数）平行的直线的普通方程。
，直线l经过点P（2,2），倾斜角
。
的值。
上各点的纵坐标压缩至原来的
，所得曲线记作C;将直线3x-2y-8=0
辆 
辆 
辆 
辆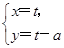 
(t为参数)过椭圆C：
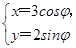(φ为参数)的右顶点，求常数a的值．