题目内容
设数列 满足
满足 ,若数列
,若数列 满足:
满足: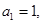 ,且当
,且当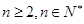 时,
时,
(I) 求 及
及 ;
;
(II)证明: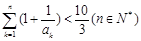 ,(注:
,(注: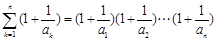 ).
).
 满足
满足 ,若数列
,若数列 满足:
满足: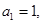 ,且当
,且当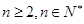 时,
时,
(I) 求
 及
及 ;
;(II)证明:
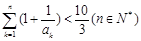 ,(注:
,(注: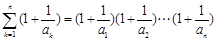 ).
).(I)
(II)注意

而
当 时,
时,


 ,即
,即 。
。

(II)注意

而

当
 时,
时,


 ,即
,即 。
。试题分析:(I)
 由
由 得
得 ,
,所以
 为等比数列;所以
为等比数列;所以
(II)由
 ,得
,得 ①
① ②; 由②-①得:
②; 由②-①得: ,则
,则 (
( )
)

当
 时,
时,


 ,即
,即
点评:典型题,本题综合性较强,处理的方法多样。涉及数列不等式的证明问题,提供了“放缩、求和、证明”和“数学归纳法”等证明方法,能拓宽学生的视野。

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
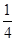 an bn,求数列{cn}的前n项和Tn.
an bn,求数列{cn}的前n项和Tn. 为等差数列,
为等差数列, +
+ +
+
 ,
,
 ,以
,以 表示
表示 项和,则使得
项和,则使得 、
、 的前
的前 项和分别为
项和分别为 、
、 ,且满足
,且满足 ,则
,则 的值为 ________.
的值为 ________. 的第二项为8,前10项和为185。
的第二项为8,前10项和为185。 项,……按原来顺序组成一个新
项,……按原来顺序组成一个新 数列,试求数列
数列,试求数列 是等差数列,公差
是等差数列,公差 ,
, 是
是 项和,已知
项和,已知 .
. ;
; =
= ,求数
,求数 列的前
列的前 .
. 中,
中, .
. 的通项公式为
的通项公式为 ,其前
,其前 项和
项和 ,则双曲线
,则双曲线 的渐近线方程为( )
的渐近线方程为( )



 :
:
 ,设
,设 ,求
,求 。
。 ,
, 为数列
为数列 的前
的前 项和,求
项和,求