题目内容
(1)解不等式9x-10•3x+9≤0;
(2)在(1)的条件下求函数f(x)=(
)x-1-4(
)x+2的最大值和最小值.
(2)在(1)的条件下求函数f(x)=(
| 1 |
| 4 |
| 1 |
| 2 |
分析:(1)利用换元法,设t=3x,从而将指数不等式转化为一元二次不等式,解不等式即可;(2)利用换元法,设t=(
)x,从而将指数复合函数问题转化为二次函数求最值问题,利用配方法求最值即可
| 1 |
| 2 |
解答:解:(1)设t=3x,则t>0,
∴不等式9x-10•3x+9≤0可转化为t2-10t+9≤0
即(t-1)(t-9)≤0,
∴1≤t≤9
即1≤3x≤9,∴0≤x≤2
∴不等式9x-10•3x+9≤0的解集为[0,2]
(2)f(x)=(
)x-1-4(
)x+2=(
)2x-2-4(
)x+2
令t=(
)x,由(1)知,0≤x≤2,∴t∈[
,1]
f(t)=4t2-4t+2,t∈[
,1]
∴当x=
时,f(t)最小=1
当x=1时,f(t)最大=2
∴函数f(x)=(
)x-1-4(
)x+2的最大值为2,最小值为1.
∴不等式9x-10•3x+9≤0可转化为t2-10t+9≤0
即(t-1)(t-9)≤0,
∴1≤t≤9
即1≤3x≤9,∴0≤x≤2
∴不等式9x-10•3x+9≤0的解集为[0,2]
(2)f(x)=(
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
令t=(
| 1 |
| 2 |
| 1 |
| 4 |
f(t)=4t2-4t+2,t∈[
| 1 |
| 4 |
∴当x=
| 1 |
| 2 |
当x=1时,f(t)最大=2
∴函数f(x)=(
| 1 |
| 4 |
| 1 |
| 2 |
点评:本题考查了指数不等式的解法,指数复合函数最值的求法,换元法在解不等式和求最值中的应用

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
 的最大值和最小值.
的最大值和最小值.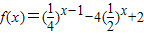 的最大值和最小值.
的最大值和最小值.