题目内容
(1)解不等式:
≤2
(2)已知不等式x2-2x+k2-1>0对一切实数x恒成立,求实数k的取值范围.
| 9 | x+4 |
(2)已知不等式x2-2x+k2-1>0对一切实数x恒成立,求实数k的取值范围.
分析:(1)移项,通分,即可求解不等式;
(2)不等式x2-2x+k2-1>0对一切实数x恒成立,等价于判别式小于0,由此可求实数k的取值范围.
(2)不等式x2-2x+k2-1>0对一切实数x恒成立,等价于判别式小于0,由此可求实数k的取值范围.
解答:解:(1)由题意,
≤0,∴
≥0,∴x<-4或x≥
∴不等式的解集为(-∞,-4)∪[
,+∞);
(2)∵不等式x2-2x+k2-1>0对一切实数x恒成立,
∴△=4-4(k2-1)<0
∴k>
或k<-
即实数k的取值范围是(-∞,-
)∪(
,+∞).
| 9-2x-8 |
| x+4 |
| 2x-1 |
| x+4 |
| 1 |
| 2 |
∴不等式的解集为(-∞,-4)∪[
| 1 |
| 2 |
(2)∵不等式x2-2x+k2-1>0对一切实数x恒成立,
∴△=4-4(k2-1)<0
∴k>
| 2 |
| 2 |
即实数k的取值范围是(-∞,-
| 2 |
| 2 |
点评:本题考查解不等式,考查恒成立问题,考查学生的计算能力,属于基础题.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
 的最大值和最小值.
的最大值和最小值.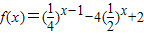 的最大值和最小值.
的最大值和最小值.