题目内容
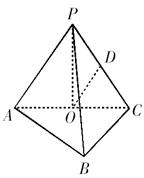
如图,四棱锥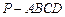 的底面
的底面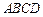 为一直角梯形,其中
为一直角梯形,其中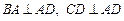 ,
, 底面
底面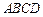 ,
,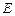 是
是 的中点.
的中点.
(1)试用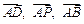 表示
表示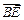 ,并判断直线
,并判断直线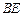 与平面
与平面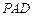 的位置关系;
的位置关系;
(2)若 平面
平面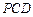 ,求异面直线
,求异面直线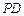 与
与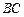 所成角的余弦值.
所成角的余弦值.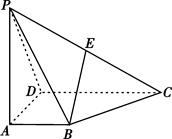
解:设 ,建立如图所示空间直角坐标系,
,建立如图所示空间直角坐标系, ,
, ,
, ,
, . ……(2分)
. ……(2分)
(1) ,
, ,
,
所以 , ……(5分)
, ……(5分) 平面
平面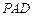 ,
, 平面
平面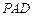 . ……(7分)
. ……(7分)
(2) 平面
平面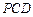 ,
, ,即
,即 .
. ,
, ,即
,即 . ……(10分)
. ……(10分) , ……(11分)
, ……(11分) ,
,
所以异面直线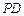 与
与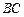 所成角的余弦值为
所成角的余弦值为 . ……(14分)
. ……(14分)
解析

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
(本题满分14分)
ABCD为矩形,CF⊥平面ABCD,DE⊥平面ABCD,AB=4a,BC= CF=2a,DE=a, P为AB的中点.
(1)求证:平面PCF⊥平面PDE;
(2)求证:AE∥平面BCF.
圆 与直线
与直线 相切于第三象限,则
相切于第三象限,则 的值是( ).
的值是( ).
A. | B. | C. | D. |
直线xtan -y=0的倾斜角是 ( )
-y=0的倾斜角是 ( )
A. | B.- | C. | D. |
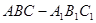 的所有棱长都为4,D为的
的所有棱长都为4,D为的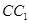 中点.
中点.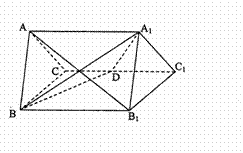
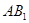 ⊥平面
⊥平面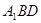 ;
;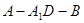 余弦值.
余弦值.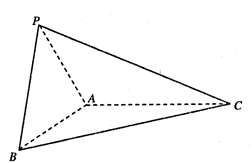
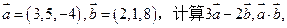 并确定
并确定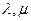 的关系,使
的关系,使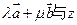 轴垂直.
轴垂直.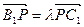 ,当 B1D⊥面PMN时,求
,当 B1D⊥面PMN时,求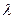 的值.
的值.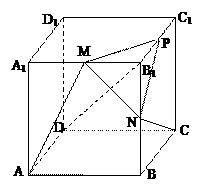
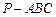 中,
中,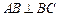 ,
,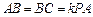 ,点
,点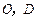 分别是
分别是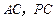 的中点,
的中点,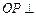 底面
底面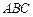 .
.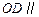 平面
平面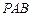 ;
;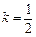 时,求直线
时,求直线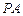 与平面
与平面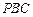 所成角的正弦值;
所成角的正弦值;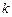 为何值时,
为何值时,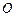 在平面
在平面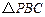 的重心.
的重心.