题目内容
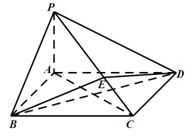
如图,三棱锥P—ABC中,平面PAC⊥平面BAC,AP=AB=AC=2,∠BAC=∠PAC=120°。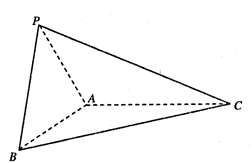
(I)求棱PB的长;
(II)求二面角P—AB—C的大小。
(I)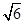 (II)
(II)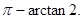
解析试题分析:(I)如图1,作PO⊥AC,垂足为O,连结OB,
由已知得,△POC≌△BOC,则BO⊥AC。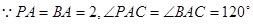 ,
,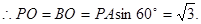
∵平面PAC⊥平面BAC,∴PO⊥平面BAC,∴PO⊥OB,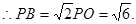
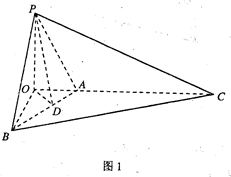
(II)方法1:如图1,作OD⊥AB,垂足为D,连结PD,由三垂线定理得,PD⊥AB。
则∠PDO为二面角P—AB—C的平面角的补角。 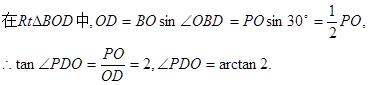
二面角P—AB—C的大小为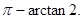
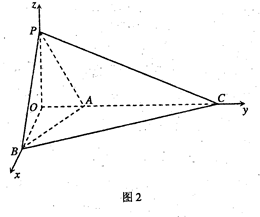
方法2:如图2,分别以OB,OC,OP为x轴,y轴,z轴,建立空间直角坐标系
O—xyz,则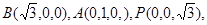

令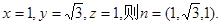
又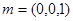 为面ABC的法向量。
为面ABC的法向量。 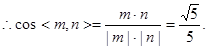
易知二面角P—AB—C的平面角为钝角,
故二面角P—AB—C的大小为
考点:线面垂直关系的判定形式及二面角的求法
点评:第二问求二面角分别用了几何法(作出二面角平面角,计算大小)和向量法(建立坐标系,写出相关点的坐标,找到两面的法向量,通过法向量的夹角找到二面角)

练习册系列答案
相关题目
已知一条直线过点(3,-2)与点(-1,-2),则这条直线的倾斜角是( ).
A. | B. | C. | D. |
 中,
中, 且
且 以
以 为折线,把
为折线,把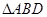 折起,使平面
折起,使平面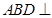 平面
平面 ,连接
,连接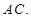
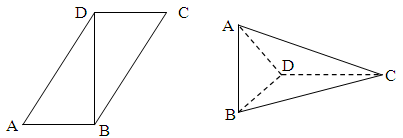
 ;
;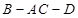 的余弦值.
的余弦值.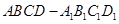 中,底面
中,底面 为平行四边形,且
为平行四边形,且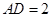 ,
,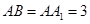 ,
,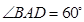 ,
, 为
为 的中点.
的中点.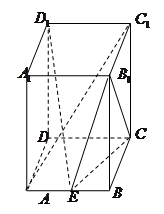
 ∥平面
∥平面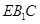 ;
;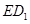 与平面
与平面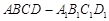 的棱长为1.应用空间向量方法求:
的棱长为1.应用空间向量方法求:
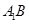 和
和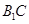 的夹角
的夹角 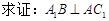 .
. 中,底面
中,底面 为矩形,
为矩形,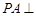 平面
平面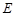 在线段
在线段 上,
上,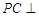 平面
平面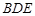 .
.
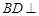 平面
平面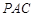 ;
; ,
, ,求二面角
,求二面角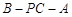 的正切值.
的正切值.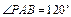 ,
,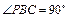 .
.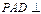 平面
平面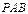 ;
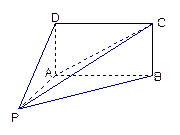
;
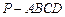 的底面
的底面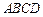 为一直角梯形,其中
为一直角梯形,其中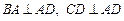 ,
, 底面
底面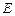 是
是 的中点.
的中点.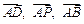 表示
表示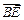 ,并判断直线
,并判断直线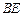 与平面
与平面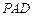 的位置关系;
的位置关系; 平面
平面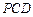 ,求异面直线
,求异面直线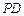 与
与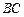 所成角的余弦值.
所成角的余弦值.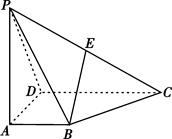
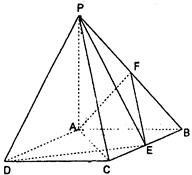
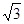 ,点F是PB的中点,点E在边BC上移动.
,点F是PB的中点,点E在边BC上移动.