题目内容
已知函数f(x)=x3-ax-1.(1)若f(x)在实数集R上单调递增,求a的取值范围;
(2)是否存在实数a,使f(x)在(-1,1)上单调递减?若存在,求出a的值;若不存在,请说明理由.
解:f′(x)=3x2-a.
(1)由3x2-a≥0在R上恒成立,即a≤3x2在R上恒成立,∴amax=0.
故当a≤0时,f(x)=x3-ax-1在R上是增函数.
(2)由3x2-a<0在(-1,1)上恒成立,∴a>3x2,但当x∈(-1,1)时,0<3x2<3,∴a≥3,即当a≥3时,f(x)在(-1,1)上单调递减.

练习册系列答案
相关题目
 ,其中
,其中 表示函数f(x)在
表示函数f(x)在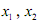 ,且
,且 ,证明:
,证明: 

 ,且f(1)=2.
,且f(1)=2. R,则下列各式成立的是
R,则下列各式成立的是