题目内容
已知函数f(x)=x-xlnx , ,其中
,其中 表示函数f(x)在
表示函数f(x)在
x=a处的导数,a为正常数.
(1)求g(x)的单调区间;
(2)对任意的正实数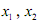 ,且
,且 ,证明:
,证明:

(3)对任意的
【答案】
见解析.
【解析】第一问中利用导数的,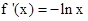 ,
, 然后判定
然后判定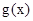 的单调性。
的单调性。
第二问中,对任意的正实数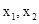 ,且
,且 ,取
,取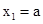 ,则
,则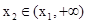 ,由(1)得
,由(1)得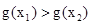 ,所以,
,所以,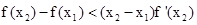
同理取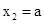 ,则
,则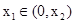 ,由(1)得
,由(1)得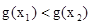 ,
,
所以,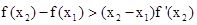 ,综合克的结论。
,综合克的结论。
第三问中,对k=1,2,3…n-2,令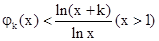 ,则
,则
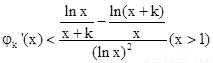 ,
,
显然1<x<x+k,,所以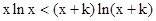 ,
,
利用放缩法证明。
解:(1)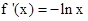 ,
,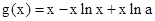 ,
,

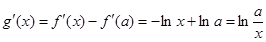 . …………………2分
. …………………2分
所以,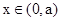 时,
时,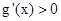 ,
,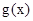 单调递增;
单调递增;
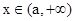 时,
时,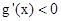 ,
,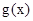 单调递减.
单调递减.
所以,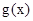 的单调递增区间为
的单调递增区间为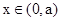 ,单调递减区间为
,单调递减区间为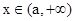 . ………4分
. ………4分
(2)(法1)对任意的正实数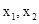 ,且
,且 ,
,
取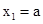 ,则
,则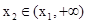 ,由(1)得
,由(1)得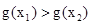 ,
,
所以,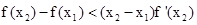 ……①;
………………………6分
……①;
………………………6分
取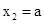 ,则
,则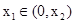 ,由(1)得
,由(1)得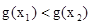 ,
,
所以,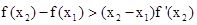 ……②.
……②.
综合①②,得结论. ………………………8分
(3)对k=1,2,3…n-2,令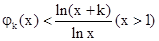 ,则
,则
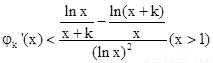 ,
,
显然1<x<x+k,,所以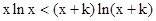 ,
,
所以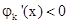 ,
,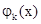 在
在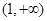 上单调递减.
上单调递减.
由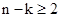 ,得
,得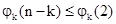 ,即
,即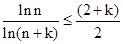 .
.
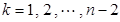 . ……………10分
. ……………10分
所以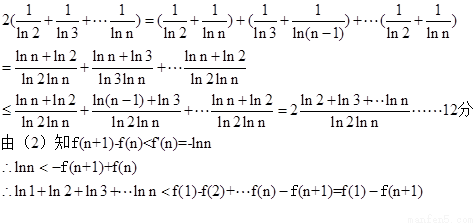
所以, .…………14分
.…………14分

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
 ,且f(1)=2.
,且f(1)=2. R,则下列各式成立的是
R,则下列各式成立的是