题目内容
已知f(x)=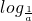 [(a-1)x-2].
[(a-1)x-2].
(1)若a>1,求f(x)的定义域;
(2)若0<a<1,判断函数f(x)的单调性,并用单调性的定义证明;
(3)若f(x)>0在[1, ]上恒成立,求a 的取值范围.
]上恒成立,求a 的取值范围.
(1)解:由a>1,a-1>0,解(a-1)x-2>0得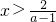
∴f(x)的定义域是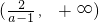 ;
;
(2)证明:∵0<a<1,a-1<0,解(a-1)x-2>0得
∴f(x)的定义域是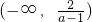
设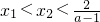 ,则
,则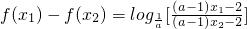
∵a-1<0,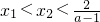
∴(a-1)x1-2>(a-1)x2-2>0
∴
∵
∴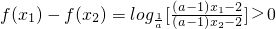
∴f(x1)-f(x2)>0
∴该函数在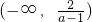 上是减函数;
上是减函数;
(3)解:①若a>1,则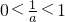 ,即在[1,
,即在[1, ]上恒有0<(a-1)x-2<1
]上恒有0<(a-1)x-2<1
∵a-1>0,∴(a-1)x-2为单调增函数,只要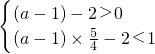 ,∴
,∴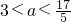
②若0<a<1,则 ,即在[1,
,即在[1, ]上恒有(a-1)x-2>1
]上恒有(a-1)x-2>1
∵a-1<0,∴(a-1)x-2为单调减函数,只要(a-1)× -2>1,∴
-2>1,∴
∵0<a<1,∴a∈∅
综上,a 的取值范围为
分析:(1)利用真数大于0,可得(a-1)x-2>0,根据a>1,得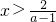 ,从而可得f(x)的定义域;
,从而可得f(x)的定义域;
(2)先求函数的f(x)的定义域是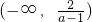 ,再利用单调性的定义,设
,再利用单调性的定义,设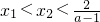 ,则
,则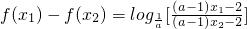 ,从而可得f(x1)-f(x2)>0,所以该函数在
,从而可得f(x1)-f(x2)>0,所以该函数在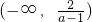 上是减函数;
上是减函数;
(3)分类讨论:①若a>1,则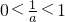 ,即在[1,
,即在[1, ]上恒有0<(a-1)x-2<1;②若0<a<1,则
]上恒有0<(a-1)x-2<1;②若0<a<1,则 ,即在[1,
,即在[1, ]上恒有(a-1)x-2>1,从而可求a 的取值范围.
]上恒有(a-1)x-2>1,从而可求a 的取值范围.
点评:本题以函数为载体,考查函数的定义域,考查函数的单调性的判断与证明,同时考查恒成立问题,解题时应注意底数的讨论.
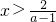
∴f(x)的定义域是
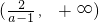 ;
;(2)证明:∵0<a<1,a-1<0,解(a-1)x-2>0得

∴f(x)的定义域是
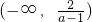
设
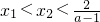 ,则
,则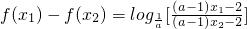
∵a-1<0,
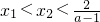
∴(a-1)x1-2>(a-1)x2-2>0
∴

∵

∴
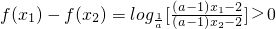
∴f(x1)-f(x2)>0
∴该函数在
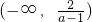 上是减函数;
上是减函数;(3)解:①若a>1,则
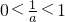 ,即在[1,
,即在[1, ]上恒有0<(a-1)x-2<1
]上恒有0<(a-1)x-2<1∵a-1>0,∴(a-1)x-2为单调增函数,只要
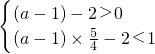 ,∴
,∴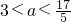
②若0<a<1,则
 ,即在[1,
,即在[1, ]上恒有(a-1)x-2>1
]上恒有(a-1)x-2>1∵a-1<0,∴(a-1)x-2为单调减函数,只要(a-1)×
 -2>1,∴
-2>1,∴
∵0<a<1,∴a∈∅
综上,a 的取值范围为

分析:(1)利用真数大于0,可得(a-1)x-2>0,根据a>1,得
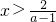 ,从而可得f(x)的定义域;
,从而可得f(x)的定义域;(2)先求函数的f(x)的定义域是
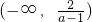 ,再利用单调性的定义,设
,再利用单调性的定义,设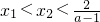 ,则
,则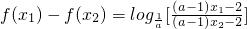 ,从而可得f(x1)-f(x2)>0,所以该函数在
,从而可得f(x1)-f(x2)>0,所以该函数在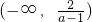 上是减函数;
上是减函数;(3)分类讨论:①若a>1,则
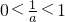 ,即在[1,
,即在[1, ]上恒有0<(a-1)x-2<1;②若0<a<1,则
]上恒有0<(a-1)x-2<1;②若0<a<1,则 ,即在[1,
,即在[1, ]上恒有(a-1)x-2>1,从而可求a 的取值范围.
]上恒有(a-1)x-2>1,从而可求a 的取值范围.点评:本题以函数为载体,考查函数的定义域,考查函数的单调性的判断与证明,同时考查恒成立问题,解题时应注意底数的讨论.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目