题目内容
已知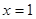 是
是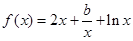 的一个极值点.
的一个极值点.
(Ⅰ) 求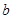 的值;
的值;
(Ⅱ) 求函数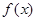 的单调递减区间;
的单调递减区间;
(Ⅲ)设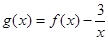 ,试问过点
,试问过点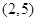 可作多少条直线与曲线
可作多少条直线与曲线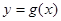 相切?请说明理由.
相切?请说明理由.
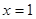 是
是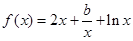 的一个极值点.
的一个极值点.(Ⅰ) 求
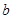 的值;
的值; (Ⅱ) 求函数
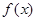 的单调递减区间;
的单调递减区间;(Ⅲ)设
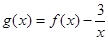 ,试问过点
,试问过点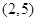 可作多少条直线与曲线
可作多少条直线与曲线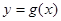 相切?请说明理由.
相切?请说明理由. (Ⅰ)3;(Ⅱ) ;(Ⅲ)2条.
;(Ⅲ)2条.
 ;(Ⅲ)2条.
;(Ⅲ)2条.试题分析:(Ⅰ)先对原函数求导,则
 ,即得
,即得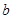 的值;(Ⅱ)求当
的值;(Ⅱ)求当 时的
时的 的取值范围,就得函数的单调减区间;(Ⅲ)易知
的取值范围,就得函数的单调减区间;(Ⅲ)易知 ,设过点(2,5)与曲线
,设过点(2,5)与曲线 相切的切点为
相切的切点为 ,
,所以
 ,
, ,令
,令 ,利用导数求函数
,利用导数求函数 的单调区间及极值,可得
的单调区间及极值,可得 与
与 轴的交点个数,从而得结论.
轴的交点个数,从而得结论.试题解析:(I)因为
 是
是 的一个极值点,所
的一个极值点,所 ,
,经检验,适合题意,所以
 . 3分
. 3分(II)定义域为
 ,
, ,
,所以函数的单调递减区间为
 6分
6分(III)
 ,设过点(2,5)与曲线
,设过点(2,5)与曲线 相切的切点为
相切的切点为
所以
 ,
, 9分
9分令
 ,所
,所 在
在 上单调递减,在
上单调递减,在 上单调递增,
上单调递增,因为
 ,所以
,所以 与x轴有两个交点,
与x轴有两个交点,所以过点
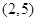 可作2条直线与曲线
可作2条直线与曲线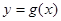 相切. 12分
相切. 12分
练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
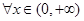 都有
都有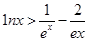 。
。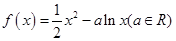 .
.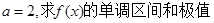 .
.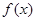 在
在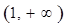 上是增函数,求
上是增函数,求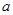 的取值范围.
的取值范围.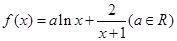 .
.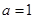 时,求
时,求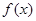 在
在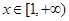 最小值;
最小值;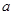 的取值范围;
的取值范围;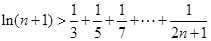 (
(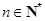 ).
).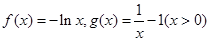 .
.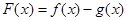 的极值,并证明:若
的极值,并证明:若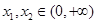 有
有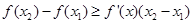 ;
; 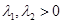 ,且
,且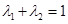 ,
,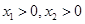 ,证明:
,证明: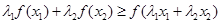 ,
,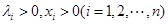 ,由上述结论猜想一个一般性结论(不需要证明);
,由上述结论猜想一个一般性结论(不需要证明);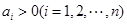 ,则
,则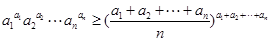 .
.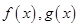 都是定义在
都是定义在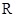 上的函数,
上的函数,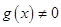 ,
,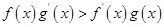 ,
,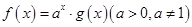 ,
,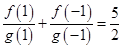 ,在有穷数列
,在有穷数列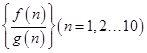 中,任意取正整数
中,任意取正整数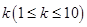 ,则前
,则前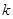 项和大于
项和大于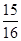 的概率是 ( )
的概率是 ( )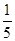
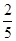
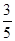
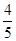
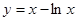
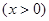 的单调递增区间是 .
的单调递增区间是 . ,则函数
,则函数 的单调递增区间是________.
的单调递增区间是________.