题目内容
已知两点A(-2,0)、B(0,2),点C是圆x2+y2-2x=0上的任意一点,则△ABC面积的最小值是
A.3-![]() B.3+
B.3+![]()
C.![]() D.
D.![]()
A
解析:
本题考查几何法求最值.
∵|AB|=2![]() 为定值,要使△ABC面积最小,只需过圆心(1,0)作直线AB的垂线,与圆的交点即为点C.又直线AB:x-y+2=0,圆心(1,0)到直线的距离为
为定值,要使△ABC面积最小,只需过圆心(1,0)作直线AB的垂线,与圆的交点即为点C.又直线AB:x-y+2=0,圆心(1,0)到直线的距离为
d=![]() =
=![]()
![]() ,
,
∴(S△ABC)min=![]() |AB|·(d-r)
|AB|·(d-r)
=![]() ·2
·2![]() ·(
·(![]() -1)=3-
-1)=3-![]() .
.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
已知两点A(-2,0),B(0,2),点C是圆x2+y2-4x+4y+6=0上任意一点,则点C到直线AB距离的最小值是
( )
( )
A、2
| ||
B、3
| ||
C、3
| ||
D、4
|
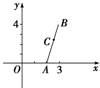 如图所示,已知两点A(2,0),B(3,4),直线ax-2y=0与线段AB交于点C,且C分
如图所示,已知两点A(2,0),B(3,4),直线ax-2y=0与线段AB交于点C,且C分