题目内容
已知两点A(-2,0),B(2,0),动点P在y轴上的射影是H,且| PA |
| PB |
| PH2 |
(1)求动点P的轨迹C的方程(6分)
(2)已知过点B的直线l交曲线C于x轴下方不同的两点M,N,求直线l的斜率的取值范围(6分)
分析:(1)设出点P的坐标(x,y),求出题中所需要的向量代入
•
=2
,即可得到x,y的关系式,即得到动点P的轨迹C的方程.
(2)分情况讨论斜率不存在、斜率为0与斜率存在但是不为0的三种情况,当斜率存在且不为0时,联立直线与双曲线的方程得到一元二次方程,再结合实根分别可得关于k的不等式组,进而求出k的取值范围即可.
| PA |
| PB |
| PH2 |
(2)分情况讨论斜率不存在、斜率为0与斜率存在但是不为0的三种情况,当斜率存在且不为0时,联立直线与双曲线的方程得到一元二次方程,再结合实根分别可得关于k的不等式组,进而求出k的取值范围即可.
解答:解(1)设P(x,y),则
=(-2-x,-y),
=(2-x,-y),
=(-x,0),
因为
•
=2
所以得y2-x2=4
(2)①若直线l的斜率不存在,直线l的方程为x=2,它与曲线C在x轴下方的部分只有一个交点(2,-2
)
②若直线l的斜率为0,则直线l是x轴,它与曲线C无交点,所以,以上两种情形与题设不符.
③设直线l之方程为y=k (x-2)(k≠0)
联立
消去x得(k2-1)y2-4ky=8k2=0
设M (x1,y1),N (x2,y2)
则M,N在x轴下方?
解出
<k<1,
∴k∈(
,1)
| PA |
| PB |
| PH |
因为
| PA |
| PB |
| PH2 |
所以得y2-x2=4
(2)①若直线l的斜率不存在,直线l的方程为x=2,它与曲线C在x轴下方的部分只有一个交点(2,-2
| 2 |
②若直线l的斜率为0,则直线l是x轴,它与曲线C无交点,所以,以上两种情形与题设不符.
③设直线l之方程为y=k (x-2)(k≠0)
联立
|
设M (x1,y1),N (x2,y2)
则M,N在x轴下方?
|
解出
| ||
| 2 |
∴k∈(
| ||
| 2 |
点评:解决此类问题的关键是对直线的斜率进行讨论,当斜率存在时正确分析题意再联立方程进而进行准确的运算,讨论圆锥曲线与直线的交点问题是这部分的一个重点内容.

练习册系列答案
相关题目
已知两点A(-2,0),B(0,2),点C是圆x2+y2-4x+4y+6=0上任意一点,则点C到直线AB距离的最小值是
( )
( )
A、2
| ||
B、3
| ||
C、3
| ||
D、4
|
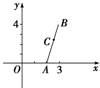 如图所示,已知两点A(2,0),B(3,4),直线ax-2y=0与线段AB交于点C,且C分
如图所示,已知两点A(2,0),B(3,4),直线ax-2y=0与线段AB交于点C,且C分