题目内容
已知函数f(x)满足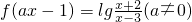 .
.
(1)求f(x)的表达式;
(2)求f(x)的定义域;
(3)判定f(x)的奇偶性与实数a之间的关系,并说明理由.
解:(1)设ax-1=t则x=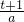 ,
,
由于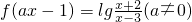 ,
,
∴ =
=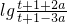 ,
,
从而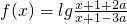 (4分)
(4分)
(2)a>0时,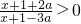 ?x∈(-∞,-2a-1)∪(3a-1,+∞),
?x∈(-∞,-2a-1)∪(3a-1,+∞),
即函数的定义域为(-∞,-2a-1)∪(3a-1,+∞),
a<0时,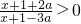 ?x∈(-∞,3a-1)∪(-2a-1,+∞).
?x∈(-∞,3a-1)∪(-2a-1,+∞).
即定义域为(-∞,3a-1)∪(-2a-1,+∞). (8分)
(3)当定义域关于原点对称时a=2,此时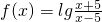 (10分)
(10分)
∵ ,∴f(x)为奇函数,(13分)
,∴f(x)为奇函数,(13分)
当a≠0且a≠2时,f(x)的定义域不关于原点对称,
故f(x)为非奇非偶函数. (15分)
分析:(1)令ax-1=t则x=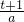 ,再利用条件:“
,再利用条件:“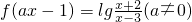 ”将其中的ax-1用t进行代换即可得出f(t),从而得出f(x)的表达式;
”将其中的ax-1用t进行代换即可得出f(t),从而得出f(x)的表达式;
(2)对a进行分类讨论:a>0时,a<0时,再利用对数的真数为正数即可得出函数的定义域;
(3)利用 (1)求得的函数的定义域,当定义域关于原点对称时a=2,此时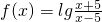 为奇函数;当a≠0且a≠2时,f(x)的定义域不关于原点对称,f(x)为非奇非偶函数.
为奇函数;当a≠0且a≠2时,f(x)的定义域不关于原点对称,f(x)为非奇非偶函数.
点评:本小题主要考查函数解析式的求解及常用方法、函数单调性的应用、函数奇偶性、不等式的解法等基础知识,考查运算求解能力,考查化归与转化思想.属于基础题.
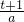 ,
,由于
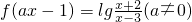 ,
,∴
 =
=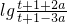 ,
,从而
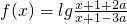 (4分)
(4分)(2)a>0时,
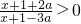 ?x∈(-∞,-2a-1)∪(3a-1,+∞),
?x∈(-∞,-2a-1)∪(3a-1,+∞),即函数的定义域为(-∞,-2a-1)∪(3a-1,+∞),
a<0时,
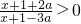 ?x∈(-∞,3a-1)∪(-2a-1,+∞).
?x∈(-∞,3a-1)∪(-2a-1,+∞). 即定义域为(-∞,3a-1)∪(-2a-1,+∞). (8分)
(3)当定义域关于原点对称时a=2,此时
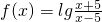 (10分)
(10分)∵
 ,∴f(x)为奇函数,(13分)
,∴f(x)为奇函数,(13分)当a≠0且a≠2时,f(x)的定义域不关于原点对称,
故f(x)为非奇非偶函数. (15分)
分析:(1)令ax-1=t则x=
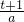 ,再利用条件:“
,再利用条件:“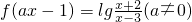 ”将其中的ax-1用t进行代换即可得出f(t),从而得出f(x)的表达式;
”将其中的ax-1用t进行代换即可得出f(t),从而得出f(x)的表达式;(2)对a进行分类讨论:a>0时,a<0时,再利用对数的真数为正数即可得出函数的定义域;
(3)利用 (1)求得的函数的定义域,当定义域关于原点对称时a=2,此时
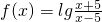 为奇函数;当a≠0且a≠2时,f(x)的定义域不关于原点对称,f(x)为非奇非偶函数.
为奇函数;当a≠0且a≠2时,f(x)的定义域不关于原点对称,f(x)为非奇非偶函数.点评:本小题主要考查函数解析式的求解及常用方法、函数单调性的应用、函数奇偶性、不等式的解法等基础知识,考查运算求解能力,考查化归与转化思想.属于基础题.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目