题目内容
7.设数列{an}是等差数列,a1=2,且a2,a3,a4+1成等比数列.(1)求数列{an}的通项公式an;
(2)设bn=$\frac{1}{{{a}_{n}}^{2}-1}$,数列{bn}的前n项和为Sn,求证:Sn$<\frac{1}{2}$.
分析 (1)利用等差数列与等比数列的通项公式即可得出.
(2)bn=$\frac{1}{{{a}_{n}}^{2}-1}$=$\frac{1}{4{n}^{2}-1}$=$\frac{1}{2}(\frac{1}{2n-1}-\frac{1}{2n+1})$,利用“裂项求和”即可得出.
解答 (1)解:设等差数列{an}的公差为d,∵a1=2,且a2,a3,a4+1成等比数列.
∴${a}_{3}^{2}$=a2•(a4+1),
∴(2+2d)2=(2+d)(2+3d+1),
化为d2-d-2=0,
解得d=2或-1.
当d=-1时,a3=0舍去.
∴d=2.
∴an=2+2(n-1)=2n.
(2)证明:bn=$\frac{1}{{{a}_{n}}^{2}-1}$=$\frac{1}{4{n}^{2}-1}$=$\frac{1}{2}(\frac{1}{2n-1}-\frac{1}{2n+1})$,
∴数列{bn}的前n项和为Sn=$\frac{1}{2}[(1-\frac{1}{3})+(\frac{1}{3}-\frac{1}{5})$+…+$(\frac{1}{2n-1}-\frac{1}{2n+1})]$
=$\frac{1}{2}(1-\frac{1}{2n+1})$$<\frac{1}{2}$,
∴Sn$<\frac{1}{2}$.
点评 本题考查了等差数列与等比数列的通项公式、“裂项求和”方法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.已知a,b,c为△ABC的三个内角A,B,C的对边,向量$\overrightarrow{m}$=($\sqrt{3}$,-1),$\overrightarrow{n}$=(cosA,sinA),若$\overrightarrow{m}$⊥$\overrightarrow{n}$,则角A的值为( )
| A. | $\frac{π}{3}$ | B. | $\frac{π}{2}$ | C. | $\frac{π}{6}$ | D. | $\frac{5π}{6}$ |
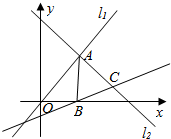 在平面直角坐标系xOy中,设直线l1:kx-y=0,直线l2:(2k-1)x+(k-1)y-7k+4=0.
在平面直角坐标系xOy中,设直线l1:kx-y=0,直线l2:(2k-1)x+(k-1)y-7k+4=0.