题目内容
A、B为椭圆x2+
解:设A、B、P三点到椭圆右准线的距离分别为d1、d2、d,则由椭圆的第二定义及几何性质得:
|AF2|=ed1=![]() d1,|BF2|=
d1,|BF2|=![]() d2,
d2,
d=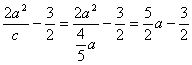 .
.
又2d=d1+d2,∴5a-3=2d.
又![]() a=|AF2|+|BF2|=
a=|AF2|+|BF2|=![]() (d1+d2),
(d1+d2),
∴d1+d2=2a.∴5a-3=2a,
∴a=1,
∴该椭圆的方程为x2+![]() y2=1.
y2=1.

练习册系列答案
相关题目
题目内容
A、B为椭圆x2+
解:设A、B、P三点到椭圆右准线的距离分别为d1、d2、d,则由椭圆的第二定义及几何性质得:
|AF2|=ed1=![]() d1,|BF2|=
d1,|BF2|=![]() d2,
d2,
d=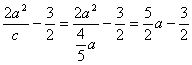 .
.
又2d=d1+d2,∴5a-3=2d.
又![]() a=|AF2|+|BF2|=
a=|AF2|+|BF2|=![]() (d1+d2),
(d1+d2),
∴d1+d2=2a.∴5a-3=2a,
∴a=1,
∴该椭圆的方程为x2+![]() y2=1.
y2=1.
