题目内容
7.设E,F分别是边长为1的正方形ABCD的边BC,CD上的点,∠EAF=45°,则$\overrightarrow{AE}$•$\overrightarrow{AF}$的最小值等于( )| A. | $\sqrt{2}$ | B. | 1 | C. | 2($\sqrt{2}$-1) | D. | $\sqrt{2}$-1 |
分析 以A为坐标原点,AB,AD所在的直线为x,y轴建立直角坐标系,设E(1,m),F(n,1),求得tan∠EAB=m,tan∠FAD=n,由两角和的正切公式可得tan(∠EAB+∠FAD)=1,即有m+n+mn=1,运用基本不等式可得mn≤($\frac{n+m}{2}$)2,解m+n的不等式即可得到所求最小值.
解答 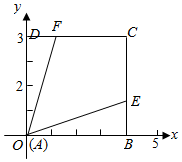 解:以A为坐标原点,AB,AD所在的直线为x,y轴建立直角坐标系,
解:以A为坐标原点,AB,AD所在的直线为x,y轴建立直角坐标系,
设E(1,m),F(n,1),
tan∠EAB=m,tan∠FAD=n,
且tan(∠EAB+∠FAD)=tan(90°-∠EAF)=tan45°=1,
即有$\frac{tan∠EAB+tan∠FAD}{1-tan∠EAB•tan∠FAD}$=$\frac{m+n}{1-mn}$=1,
即为m+n+mn=1,
则$\overrightarrow{AE}$•$\overrightarrow{AF}$=(1,m)•(n,1)=m+n,
由mn≤($\frac{n+m}{2}$)2,可得1=m+n+mn≤(m+n)+$\frac{(m+n)^{2}}{4}$,
解不等式可得m+n≥2($\sqrt{2}$-1),
当且仅当m=n时,$\overrightarrow{AE}$•$\overrightarrow{AF}$的最小值为2($\sqrt{2}$-1),
故选:C.
点评 本题考查向量的数量积的坐标表示和最值的求法,注意运用基本不等式和两角和的正切公式,考查化简整理的运算能力,属于中档题.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
19.各项均不为零的等差数列{an}中,若an+1=an2-an-1(n∈N*,n≥2),则S2016=( )
| A. | 0 | B. | 2 | C. | 2015 | D. | 4032 |
