题目内容
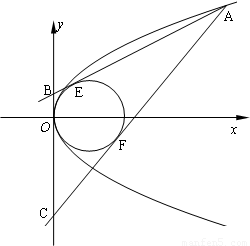
已知A是抛物线y2=2x上的一动点,过A作圆(x-1)2+y2=1的两条切线分别切圆于E、F两点,交y轴于B、C两点.(1)当A点的坐标为(8,4)时,求直线EF的方程.
(2)当A点的横坐标大于2时,求△ABC的面积的最小值.
【答案】分析:(1)圆:(x-1)2+y2=1的圆心C(1,0),所以以AC为直径的圆为:x2+y2-9x-4y+8=0,结合题意证明点E、F在圆x2+y2-9x-4y+8=0上,所以E、F两点是两个圆的交点,两个圆的方程相减即可得到直线EF的方程.
(2)设B(0,yB),C(0,yC),A(xO,yO),其中x>2,写出直线AB的方程为(yO-yB)x-xOy+xOyB=0,由直线AB与圆相切可得(xO-2)yB2+2yOyB-xO=0,同理:(xO-2)yA2+2yOyA-xO=0,故yA,yB是方程(xO-2)y2+2yOy-xO=0的两个不同的实根,因为 ,再结合韦达定理即可求出三角形的最小值.
,再结合韦达定理即可求出三角形的最小值.
解答:解:(1)由题意可得:圆:(x-1)2+y2=1的圆心C(1,0),
所以以线段AC为直径的圆的方程为:x2+y2-9x-4y+8=0.
因为AE⊥CE,AF⊥CF,
所以点E、F在圆x2+y2-9x-4y+8=0上,
所以E、F两点是两个圆的交点.
所以所求圆的方程与圆:(x-1)2+y2=1相减,消去二次项,就得公共弦EF所在的直线方程,
所以直线EF的方程为7x+4y-8=0.
(2)设B(0,yB),C(0,yC),A(xO,yO),其中x>2,
所以直线AB的方程为 ,化简得(yO-yB)x-xOy+xOyB=0
,化简得(yO-yB)x-xOy+xOyB=0
直线AB与圆相切,故 ,两边平方化简得(xO-2)yB2+2yOyB-xO=0
,两边平方化简得(xO-2)yB2+2yOyB-xO=0
同理可得:(xO-2)yA2+2yOyA-xO=0,
故yC,yB是方程(xO-2)y2+2yOy-xO=0的两个不同的实根, ,
,
因为
所以 =
= ,
,
所以当且仅当xO=4时,S取到最小值8,
所以△ABC的面积的最小值为8.
点评:本题主要考查直线与抛物线的位置关系,以及圆与圆的位置关系,而解决直线与圆锥曲线的位置关系有关的问题,一般的思路是将直线与圆锥曲线方程联立,利用韦达定理来找突破口.
(2)设B(0,yB),C(0,yC),A(xO,yO),其中x>2,写出直线AB的方程为(yO-yB)x-xOy+xOyB=0,由直线AB与圆相切可得(xO-2)yB2+2yOyB-xO=0,同理:(xO-2)yA2+2yOyA-xO=0,故yA,yB是方程(xO-2)y2+2yOy-xO=0的两个不同的实根,因为
 ,再结合韦达定理即可求出三角形的最小值.
,再结合韦达定理即可求出三角形的最小值.解答:解:(1)由题意可得:圆:(x-1)2+y2=1的圆心C(1,0),
所以以线段AC为直径的圆的方程为:x2+y2-9x-4y+8=0.
因为AE⊥CE,AF⊥CF,
所以点E、F在圆x2+y2-9x-4y+8=0上,
所以E、F两点是两个圆的交点.
所以所求圆的方程与圆:(x-1)2+y2=1相减,消去二次项,就得公共弦EF所在的直线方程,
所以直线EF的方程为7x+4y-8=0.
(2)设B(0,yB),C(0,yC),A(xO,yO),其中x>2,
所以直线AB的方程为
 ,化简得(yO-yB)x-xOy+xOyB=0
,化简得(yO-yB)x-xOy+xOyB=0直线AB与圆相切,故
 ,两边平方化简得(xO-2)yB2+2yOyB-xO=0
,两边平方化简得(xO-2)yB2+2yOyB-xO=0同理可得:(xO-2)yA2+2yOyA-xO=0,
故yC,yB是方程(xO-2)y2+2yOy-xO=0的两个不同的实根,
 ,
,
因为

所以
 =
= ,
,所以当且仅当xO=4时,S取到最小值8,
所以△ABC的面积的最小值为8.
点评:本题主要考查直线与抛物线的位置关系,以及圆与圆的位置关系,而解决直线与圆锥曲线的位置关系有关的问题,一般的思路是将直线与圆锥曲线方程联立,利用韦达定理来找突破口.

练习册系列答案
相关题目
已知M是抛物线y2=2px(p>0)上的点,若M到此抛物线的准线和对称轴的距离分别为5和4,则点M的横坐标为( )
| A、1 | B、1或4 | C、1或5 | D、4或5 |
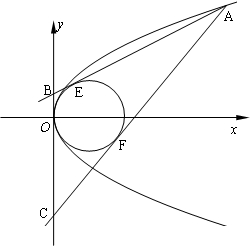 已知A是抛物线y2=2x上的一动点,过A作圆(x-1)2+y2=1的两条切线分别切圆于E、F两点,交y轴于B、C两点.
已知A是抛物线y2=2x上的一动点,过A作圆(x-1)2+y2=1的两条切线分别切圆于E、F两点,交y轴于B、C两点.