题目内容
已知A是抛物线y2=4x上一点,F是抛物线的焦点,直线FA交抛物线的准线于点B(点B在x轴上方),若|AB|=2|AF|,则点A的坐标为 .
分析:设B(-1,t),A(m,n),则根据|AB|=2|AF|(点B在x轴上方),可得
=2
(n>0)或
=
(n<0),分类讨论,即可求得点A的坐标.
| BA |
| AF |
| BF |
| FA |
解答:解:设B(-1,t),A(m,n),则
∵抛物线y2=4x,
∴F(1,0),
∵|AB|=2|AF|(点B在x轴上方),
∴
=2
(n>0)或
=
(n<0),
=2
(n>0)时,(m+1,n-t)=2(1-m,-n),
∴
,
∴m=
,代入y2=4x可得n=
;
=
(n<0)时,(m+1,n-t)=2(m-1,n),
∴m=3,代入y2=4x可得n=-2
.
∴点A的坐标为(3, -2
)或(
,
).
故答案为:(3, -2
)或(
,
).
∵抛物线y2=4x,
∴F(1,0),
∵|AB|=2|AF|(点B在x轴上方),
∴
| BA |
| AF |
| BF |
| FA |
| BA |
| AF |
∴
|
∴m=
| 1 |
| 3 |
2
| ||
| 3 |
| BF |
| FA |
∴m=3,代入y2=4x可得n=-2
| 3 |
∴点A的坐标为(3, -2
| 3 |
| 1 |
| 3 |
2
| ||
| 3 |
故答案为:(3, -2
| 3 |
| 1 |
| 3 |
2
| ||
| 3 |
点评:本题考查抛物线的性质,考查向量知识的运用,考查分类讨论的数学思想,属于中档题.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
已知M是抛物线y2=2px(p>0)上的点,若M到此抛物线的准线和对称轴的距离分别为5和4,则点M的横坐标为( )
| A、1 | B、1或4 | C、1或5 | D、4或5 |
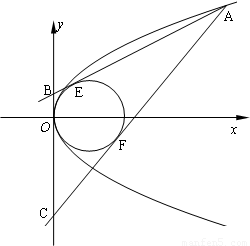
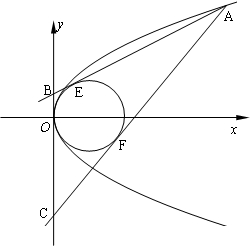 已知A是抛物线y2=2x上的一动点,过A作圆(x-1)2+y2=1的两条切线分别切圆于E、F两点,交y轴于B、C两点.
已知A是抛物线y2=2x上的一动点,过A作圆(x-1)2+y2=1的两条切线分别切圆于E、F两点,交y轴于B、C两点.