Question

1．某校为了响应《中共中央国务院关于加强青少年体育增强青少年体质的意见》精神，落实“生命-和谐”教育理念和阳光体育行动的现代健康理念，学校特组织“踢毽球”大赛，某班为了选出一人参加比赛，对班上甲乙两位同学进行了8次测试，且每次测试之间是相互独立的．成绩如下：（单位：个/分钟）

甲	80	81	93	72	88	75	83	84
乙	82	93	70	84	77	87	78	85

（1）用茎叶图表示这两组数据；
（2）从统计学的角度考虑，你认为选派哪位学生参加比赛合适，请说明理由；
（3）分别估计该班对甲乙两同学的成绩高于79个/分钟的概率
（参考数据：2²+1²+11²+10²+6²+7²+1²+2²=316，0²+11²+12²+2²+5²+5²+4²+3²=344）

Answer 1

分析 （1）以十位数为茎，个位数为叶，能作出表示这两组数据的茎叶图．
（2）分别求出甲、乙两组数扭的平均数和方差，由于甲乙的平均成绩相等，而甲的方差较小，所以甲的成绩较稳定，派甲参赛比较合适．
（3）由已知条件利用等可能事件概率计算公式能求出该班对甲乙两同学的成绩高于79个/分钟的概率．

解答 解：（1）以十位数为茎，个位数为叶，能作出表示这两组数据的茎叶图：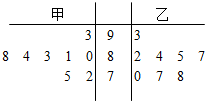

…（4分）
（2）$\overline{x_甲}=\frac{80+81+93+72+88+75+83+84}{8}=82$，
$\overline{x_乙}=\frac{82+93+70+84+77+87+78+85}{8}=82$，
$S_甲^2=\frac{{{2^2}+{1^2}+{{11}^2}+{{10}^2}+{6^2}+{7^2}+{1^2}+{2^2}}}{8}=39.5$，
$S_乙^2=\frac{{{0^2}+{{11}^2}+{{12}^2}+{2^2}+{5^2}+{5^2}+{4^2}+{3^2}}}{8}=43$
由于甲乙的平均成绩相等，而甲的方差较小，所以甲的成绩较稳定，派甲参赛比较合适…（8分）
注：本小题的结论及理由不唯一，如果考生从统计学的角度分析，给出其他合理回答，同样给分；
如派甲比较合适，理由如下：甲获得79个/分钟以上的概率为${P_1}=\frac{6}{8}=\frac{3}{4}$，
乙获得79个/分钟以上的概率为${P_2}=\frac{5}{8}$．∵P₁＞P₂，所以派甲参赛比较合适．
（3）甲获得79个/分钟以上的概率为${P_1}=\frac{6}{8}=\frac{3}{4}$，乙获得79个/分钟以上的概率为${P_2}=\frac{5}{8}$．…（12分）

点评 本题考查概率的求法，考查平均数、方差的性质的应用，考查茎叶图的作法，是基础题，解题时要认真审题，注意等可能事件概率计算公式的合理运用．