题目内容
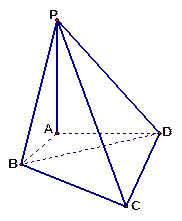
在四棱锥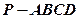 ,
,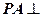 平面
平面 ,
,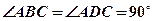 ,
,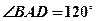 ,
, ,
,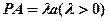 .
.
(1)求证:平面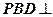 平面
平面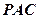 ;
;
(2)当点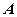 到平面
到平面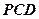 的距离为
的距离为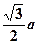 时,求二面角
时,求二面角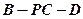 的余弦值;
的余弦值;
(3)当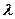 为何值时,点
为何值时,点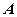 在平面
在平面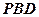 内的射影
内的射影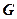 恰好是
恰好是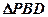 的重心.
的重心.
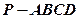 ,
,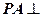 平面
平面 ,
,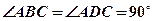 ,
,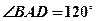 ,
, ,
,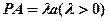 .
.
(1)求证:平面
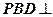 平面
平面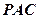 ;
;(2)当点
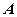 到平面
到平面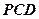 的距离为
的距离为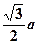 时,求二面角
时,求二面角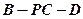 的余弦值;
的余弦值;(3)当
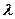 为何值时,点
为何值时,点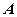 在平面
在平面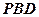 内的射影
内的射影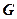 恰好是
恰好是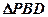 的重心.
的重心.(1)连接
 交
交 于
于 ,易知
,易知 ,而
,而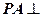 面
面 ,
, ,
,又
 面
面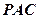 ,又
,又 面
面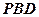 ,
, 平面
平面 平面
平面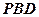 (4分)
(4分)(2)由
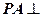 面
面 得
得 ,又
,又 ,
, 面
面
又
 面
面 面
面
 面
面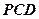 (5分)
(5分)过
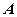 作
作 于
于 面
面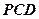 ,
, 是点
是点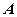 到平面
到平面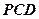 的距离(6分)故
的距离(6分)故
 (8分)所以
(8分)所以
作
 于
于 ,连接
,连接 ,
, ,
, 为所求
为所求在
 ,
,
(3)连接
 ,则重心
,则重心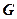 在
在 上,且
上,且 ,连接
,连接 (9分)
(9分)已知
 面
面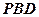 ,所以
,所以 (10分),
(10分),由
 可得
可得 ,解得
,解得
略

练习册系列答案
相关题目
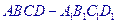 ,
,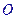 是底
是底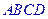 对角线的交点.
对角线的交点.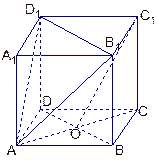
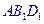 ;
;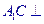 面
面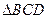 与
与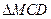 都是边长为2的正三角形,平面
都是边长为2的正三角形,平面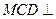 平面
平面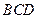 ,
,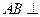 平面BCD,
平面BCD,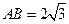 .求点A到平面MBC的距离。
.求点A到平面MBC的距离。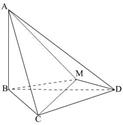
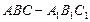 中,
中,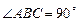 ,
,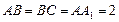 。
。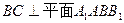 ;(2)已知
;(2)已知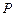 是棱
是棱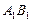 上的一动点,问:三棱锥
上的一动点,问:三棱锥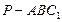 的体积是否为定值,如不是定值,请说明理由;如是定值,请求出此定值。
的体积是否为定值,如不是定值,请说明理由;如是定值,请求出此定值。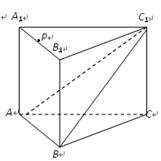
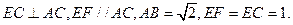

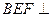 平
平 面DEF;
面DEF; 角A—BF—E的大小。
角A—BF—E的大小。 本题满分10分)
本题满分10分) 求证:a∥l.
求证:a∥l.

 中,若
中,若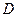 是
是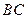 的中点,
的中点,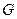 是
是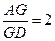 ”.若把该结论推广到空间,则有结论:“在六条棱长都相等
”.若把该结论推广到空间,则有结论:“在六条棱长都相等 的四面体
的四面体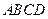 中,若
中,若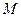 是
是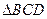 的三边中线的交点,
的三边中线的交点,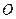 为四面体
为四面体 ”
”