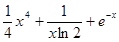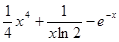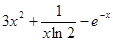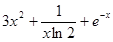题目内容
设函数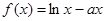 ,
, ,其中
,其中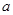 为实数,若
为实数,若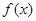 在
在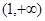 上是单调减函数,且
上是单调减函数,且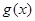 在
在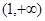 上有最小值,求
上有最小值,求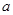 的取值范围.
的取值范围.
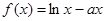 ,
, ,其中
,其中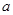 为实数,若
为实数,若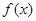 在
在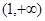 上是单调减函数,且
上是单调减函数,且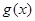 在
在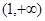 上有最小值,求
上有最小值,求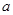 的取值范围.
的取值范围.a∈(e,+∞)
试题分析:分别利用导数求出
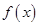 单调区间与
单调区间与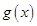 在
在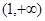 上的最小值,与给定的
上的最小值,与给定的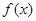 在
在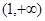 上是单调减函数,且
上是单调减函数,且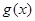 在
在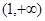 上有最小值相结合,得出关于
上有最小值相结合,得出关于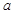 的关系式,可得
的关系式,可得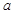 的取值范围.
的取值范围.解:令
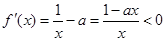 ,
,考虑到f(x)的定义域为(0,+∞),故a>0,进而解得x>a-1,即f(x)在(a-1,+∞)上是单调减函数,
同理,f(x)在(0,a-1)上是单调增函数.
由于f(x)在(1,+∞)上是单调减函数,故(1,+∞)
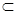 (a-1,+∞),从而a-1≤1,即a≥1,
(a-1,+∞),从而a-1≤1,即a≥1,令g'(x)=ex-a=0,得
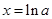 .
.当
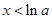 时,
时, 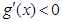 ;当x>
;当x>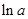 时,
时, 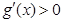 .
.又g(x)在(1,+∞)上有最小值,所以
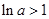 ,
,即a>e.综上,有a∈(e,+∞).
考点:利用导数求函数的单调区间与最值.

练习册系列答案
相关题目
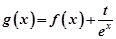 ,且A(x1,y1)、B(x2,y2)(x1≠x2)是曲线y=g(x)上任意两点,若对任意的t≤-1,直线AB的斜率恒大于常数m,求m的取值范围;
,且A(x1,y1)、B(x2,y2)(x1≠x2)是曲线y=g(x)上任意两点,若对任意的t≤-1,直线AB的斜率恒大于常数m,求m的取值范围;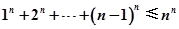 (n∈N*).
(n∈N*).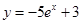 在点
在点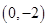 处的切线方程为________.
处的切线方程为________.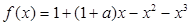 ,其中
,其中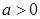 .
.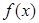 在其定义域上的单调性;
在其定义域上的单调性;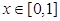 时,求
时,求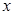 的值.
的值.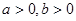 ,且函数
,且函数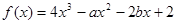 在
在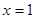 处有极值,则ab的最大值为 .
处有极值,则ab的最大值为 .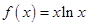 ,若
,若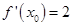 则
则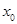 等于( )
等于( )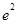
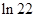
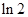
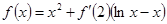 ,则
,则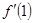 = ( )
= ( )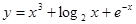 ,则
,则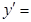 ( ).
( ).