Question

【题目】已知点是直线与椭圆的一个公共点， 分别为该椭圆的左右焦点，设取得最小值时椭圆为.

（1）求椭圆的标准方程及离心率；

（2）已知为椭圆上关于轴对称的两点， 是椭圆上异于的任意一点，直线分别与轴交于点，试判断是否为定值；如果为定值，求出该定值；如果不是，请说明理由.

Answer 1

【答案】(1) ；（2） .

【解析】试题分析：（1）联立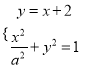，得，由此利用韦达定理、椭圆定义，结合已知条件能求出椭圆的方程；（2）设，且，由已知求出，由此能求出为定值.

试题解析：（1）联立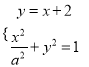，得，

∵直线与椭圆有公共点，

∴，解得，∴，

又由椭圆定义知，

故当时， 取得最小值，

此时椭圆的方程为；离心率为 ；

（2）设，且，

∵，∴，

即，

∴，

同理，得，

∴，

又，

∴，

∴，

∴为定值1.