��Ŀ����
7����ͼ�ڡ�ABC�У�$\overrightarrow{AN}$=$\frac{1}{3}$$\overrightarrow{NC}$��P��BN�ϵ�һ�㣬��$\overrightarrow{AP}$=��$\overrightarrow{AB}$+$\frac{1}{5}$$\overrightarrow{AC}$����ʵ���˵�ֵΪ��������
| A�� | $\frac{1}{5}$ | B�� | $\frac{2}{5}$ | C�� | $\frac{4}{5}$ | D�� | $\frac{3}{10}$ |
���� ��$\overrightarrow{BP}$=m$\overrightarrow{BN}$�����ǿɽ�$\overrightarrow{AP}$��ʾΪ��1-m��$\overrightarrow{AB}$+$\frac{m}{4}$$\overrightarrow{AC}$����ʽ������ƽ�������Ļ�����������������ڦˣ�m�ķ����飬�ⷽ����ɵõ��˵�ֵ��
��� �⣺��$\overrightarrow{BP}$=m$\overrightarrow{BN}$����$\overrightarrow{AN}$=$\frac{1}{3}$$\overrightarrow{NC}$����$\overrightarrow{AN}$=$\frac{1}{4}$$\overrightarrow{AC}$��
��$\overrightarrow{AP}$=$\overrightarrow{AB}+\overrightarrow{BP}$=$\overrightarrow{AB}$+m$\overrightarrow{BN}$=$\overrightarrow{AB}$+m��$\overrightarrow{AN}-\overrightarrow{AB}$��=��1-m��$\overrightarrow{AB}$+m$\overrightarrow{AN}$=��1-m��$\overrightarrow{AB}$+$\frac{m}{4}$$\overrightarrow{AC}$��
��$\overrightarrow{AP}$=��$\overrightarrow{AB}$+$\frac{1}{5}$$\overrightarrow{AC}$��
��$\left\{\begin{array}{l}{1-m=��}\\{\frac{m}{4}=\frac{1}{5}}\end{array}\right.$����æ�=$\frac{1}{5}$��
��ѡ��A��
���� ������Ҫ�����˵�֪ʶ�����������Ļ��������������壬�����Ĺؼ��Ǹ����������Ļ�������������ڦˣ�m�ķ����飬�����е��⣮

 ǧ�������������ĩ�����Ծ�����ϵ�д�
ǧ�������������ĩ�����Ծ�����ϵ�д�����������һƽ�����أ���ֳɵ������ֲ�һ����������
����������ƽ�У�������涼�����εļ��������̨��
����һ��ƽ��ȥ��Բ������ͽ���֮��IJ�����ɵļ������Բ̨��
����������ƽ�У�������涼��ƽ���ı��εļ������������
| A�� | �ۢ� | B�� | �٢� | C�� | �٢ڢ� | D�� | �� |
| A�� | $\frac{{x}^{2}}{16}+\frac{{y}^{2}}{12}=1$ | B�� | $\frac{{x}^{2}}{16}+\frac{{y}^{2}}{4}=1$ | C�� | $\frac{{x}^{2}}{12}+\frac{{y}^{2}}{8}=1$ | D�� | $\frac{{x}^{2}}{16}+\frac{{y}^{2}}{8}=1$ |
| A�� | {2��4} | B�� | {3} | C�� | {2��4��6} | D�� | {1��2��3��4��5} |
 ��ͼ����ƽ��ֱ������ϵxoy�У���ԲC�ı�����Ϊ$\frac{{x}^{2}}{6}$+$\frac{{y}^{2}}{2}$=1��ֱ��l��x�ύ�ڵ�E������ԲC����A��B���㣮
��ͼ����ƽ��ֱ������ϵxoy�У���ԲC�ı�����Ϊ$\frac{{x}^{2}}{6}$+$\frac{{y}^{2}}{2}$=1��ֱ��l��x�ύ�ڵ�E������ԲC����A��B���㣮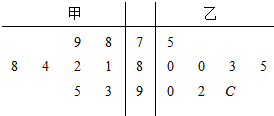 �ס������˲μ���ѧ������ѵ���ֱַ����������ѵ�ڼ�μӵ����ɴ�Ԥ���ɼ��������ȡ8�Σ�������Ҷͼ��ͼ��ʾ���ҵijɼ�����һ������λ����ģ�����ھ�Ҷͼ����c��ʾ������Ƶ�ʵ������ʣ�
�ס������˲μ���ѧ������ѵ���ֱַ����������ѵ�ڼ�μӵ����ɴ�Ԥ���ɼ��������ȡ8�Σ�������Ҷͼ��ͼ��ʾ���ҵijɼ�����һ������λ����ģ�����ھ�Ҷͼ����c��ʾ������Ƶ�ʵ������ʣ�