题目内容
【题目】已知椭圆方程为![]() ,其右焦点
,其右焦点![]() 与抛物线
与抛物线![]() 的焦点重合,过
的焦点重合,过![]() 且垂直于抛物线对称轴的直线与椭圆交于
且垂直于抛物线对称轴的直线与椭圆交于![]() 、
、![]() 两点,与抛物线交于
两点,与抛物线交于![]() 、
、![]() 两点.
两点.![]()
(1)求椭圆的方程;
(2)若直线l与(1)中椭圆相交于![]() ,
,![]() 两点, 直线
两点, 直线![]() ,
, ![]() ,
,![]() 的斜率分别为
的斜率分别为![]() ,
,![]() ,
,![]() (其中
(其中![]() ),且
),且![]() ,
,![]() ,
,![]() 成等比数列;设
成等比数列;设![]() 的面积为
的面积为![]() , 以
, 以![]() 、
、![]() 为直径的圆的面积分别为
为直径的圆的面积分别为![]() ,
, ![]() , 求
, 求![]() 的取值范围.
的取值范围.
【答案】(1) ![]() (2)
(2) ![]()
【解析】
(1)由题意可得![]() ,
,![]() ,即得
,即得![]() ,结合
,结合![]() 可得椭圆方程;(2)设直线
可得椭圆方程;(2)设直线![]() 的方程为
的方程为![]() ,将直线方程与椭圆方程联立,写出韦达定理,由
,将直线方程与椭圆方程联立,写出韦达定理,由![]() ,
,![]() ,
,![]() 成等比数列,可解得k值,然后分别求出S,
成等比数列,可解得k值,然后分别求出S,![]() ,写出
,写出![]() 的表达式,利用基本不等式可得取值范围.
的表达式,利用基本不等式可得取值范围.
(1)由抛物线方程得![]() ,椭圆方程为
,椭圆方程为![]() ,过F垂直于抛物线对称轴的直线与椭圆交于M,N两点,可得
,过F垂直于抛物线对称轴的直线与椭圆交于M,N两点,可得![]() ,与抛物线交于C,D两点可得
,与抛物线交于C,D两点可得![]() ,
, 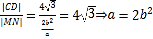 ,
, ![]() ,
,![]()
![]() ,
,
所以椭圆方程为![]() .
.
(2)设直线![]() 的方程为
的方程为![]() ,
,
由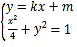 可得
可得![]() ,
,
由韦达定理: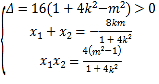 ,
,
∵![]() ,
,![]() ,
,![]() 构成等比数列,
构成等比数列,![]()
![]() ,
,
即![]()
由韦达定理代入化简得:![]() ,∵
,∵ ![]() ,
,![]()
![]() .
.
此时![]() ,即
,即![]() .
.
又由![]() 三点不共线得
三点不共线得![]() ,从而
,从而![]() .
.
故![]()
![]()
∵![]() ,
,![]() ,
,![]() ,
,
则![]()
![]() 为定值.
为定值.
![]()
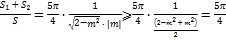 ,
,
当且仅当![]() 即
即![]() 时等号成立.
时等号成立.
综上:![]() 的取值范围是
的取值范围是![]() .
.

练习册系列答案
相关题目