题目内容
(本小题满分10分)选修4-5:不等式选讲
设函数 .
.
(1)解不等式 ;
;
(2)若 对一切实数
对一切实数 均成立,求实数
均成立,求实数 的取值范围.
的取值范围.
(1) ;(2)
;(2) .
.
【解析】
试题分析:(1)分类讨论,当 时,当
时,当 时,当
时,当 时,分别求出不等式的解集,再把解集取交集;
时,分别求出不等式的解集,再把解集取交集;
(2)由绝对值的几何意义可求得 的最小值为
的最小值为 ,从而若要使
,从而若要使 恒成立,只需
恒成立,只需 .
.
试题解析:(1)当 时,
时,  ,得
,得 ,∴
,∴ 成立,当
成立,当 时,
时, ,得
,得 ,∴
,∴ 成立,
成立,
当 时,
时,  ,得
,得 ,∴
,∴ 成立,
成立,
综上,原不等式的解集为 ; 5分
; 5分
(2) ,当
,当 或
或 时等号成立,
时等号成立,
∴ . 10分
. 10分
考点:1.绝对值不等式;2.分类讨论的数学思想.
考点分析: 考点1:含绝对值的不等式 试题属性- 题型:
- 难度:
- 考核:
- 年级:

练习册系列答案
相关题目
 则方程
则方程 的所有解之和等于 .
的所有解之和等于 . ,若
,若 ,则
,则  _______.
_______. 若△OAB是以O为
若△OAB是以O为 点的等腰直角三角形,则△AOB的面积是_______
点的等腰直角三角形,则△AOB的面积是_______ 的解集为( )
的解集为( )
 D.
D.
 的底面为菱形,且
的底面为菱形,且 ,
, ,
, .
.
 平面
平面 ;
; 的体积.
的体积. 上的函数
上的函数 满足
满足 ,
, ,则不等式
,则不等式 (
( 为自然对数的底数)的解集为( )
为自然对数的底数)的解集为( ) B.
B. C.
C. D.
D.
 ,且三人投票相互没有影响.若投票结果中至少有两张“获奖”票,则决定该节目最终获一等奖;否则,该节目不能获一等奖.
,且三人投票相互没有影响.若投票结果中至少有两张“获奖”票,则决定该节目最终获一等奖;否则,该节目不能获一等奖. 的分布列及数学期望.
的分布列及数学期望.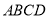 中,点
中,点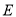 为边
为边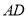 上的点,点
上的点,点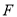 为边
为边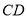 的中点,
的中点, 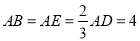 ,现将
,现将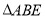 沿
沿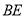 边折至
边折至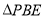 位置,且平面
位置,且平面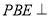 平面
平面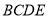 .
.
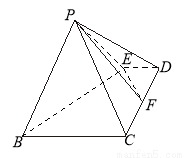
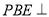 平面
平面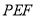 ;
;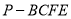 的体积.
的体积.