题目内容
已知函数f(x)=|2x-a|+|x+1|.
(Ⅰ)当a=1时,解不等式f(x)<3;
(Ⅱ)若f(x)的最小值为1,求a的值.
(Ⅰ)当a=1时,解不等式f(x)<3;
(Ⅱ)若f(x)的最小值为1,求a的值.
考点:绝对值不等式的解法
专题:不等式的解法及应用
分析:(Ⅰ)当a=1时,求出函数的分段函数形式,然后求解不等式f(x)<3的解集即可;
(Ⅱ)利用绝对值的几何意义求出f(x)的最小值的表达式,利用最小值为1,求a的值.
(Ⅱ)利用绝对值的几何意义求出f(x)的最小值的表达式,利用最小值为1,求a的值.
解答:
解:(Ⅰ)因为f(x)=|2x-1|+|x+1|=
;
且f(1)=f(-1)=3,所以,f(x)<3的解集为{x|-1<x<1};…(4分)
(Ⅱ)|2x-a|+|x+1|=|x-
|+|x+1|+|x-
|≥|1+
|+0=|1+
|
当且仅当(x+1)(x-
)≤0且x-
=0时,取等号.
所以|1+
|=1,解得a=-4或0.…(10分)
|
且f(1)=f(-1)=3,所以,f(x)<3的解集为{x|-1<x<1};…(4分)
(Ⅱ)|2x-a|+|x+1|=|x-
| a |
| 2 |
| a |
| 2 |
| a |
| 2 |
| a |
| 2 |
当且仅当(x+1)(x-
| a |
| 2 |
| a |
| 2 |
所以|1+
| a |
| 2 |
点评:本题考查绝对值不等式的解法,绝对值的几何意义的应用,考查转化是以及计算能力.

练习册系列答案
相关题目
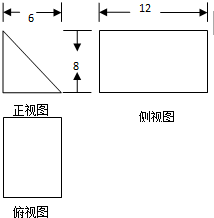 已知一块大理石表示的几何体的三视图如图所示,将该大理石切削、打磨加工成球体,则能得到的最大球体的体积为( )
已知一块大理石表示的几何体的三视图如图所示,将该大理石切削、打磨加工成球体,则能得到的最大球体的体积为( )A、
| ||
B、
| ||
| C、36π | ||
D、
|
下列四个图象中,两个变量具有正相关关系的是( )
A、 |
B、 |
C、 |
D、 |
sin
cos
tan
的值为( )
| 7π |
| 6 |
| 2π |
| 3 |
| 5π |
| 4 |
A、-
| ||||
B、
| ||||
C、
| ||||
D、-
|
已知函数f(x)=x3+x(x∈R),当0<θ≤
时,f(msinθ)+f(sinθ-sin2θ-2)<0恒成立,则实数m的取值范围是( )
| π |
| 2 |
A、(-∞,2
| ||
B、(-∞,2
| ||
| C、(-∞,3) | ||
| D、(-∞,2) |
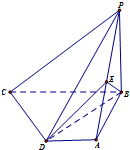 在四棱锥P-ABCD中,已知PB⊥底面ABCD,BC⊥AB,AD∥BC,AB=AD=2,CD⊥BD,异面直线PA,CD所成角等于60°
在四棱锥P-ABCD中,已知PB⊥底面ABCD,BC⊥AB,AD∥BC,AB=AD=2,CD⊥BD,异面直线PA,CD所成角等于60°