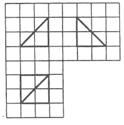
题目内容
(本题满分15分) 如图,四边形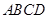 中,
中, 为正三角形,
为正三角形,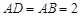 ,
, ,
, 与
与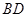 交于
交于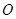 点.将
点.将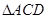 沿边
沿边 折起,使
折起,使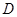 点至
点至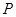 点,已知
点,已知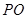 与平面
与平面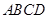 所成的角为
所成的角为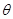 ,且
,且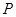 点在平面
点在平面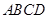 内的射影落在
内的射影落在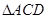 内.
内.
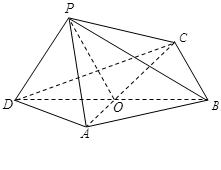
(Ⅰ)求证: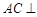 平面
平面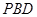 ;
;
(Ⅱ)若已知二面角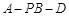 的余弦值为
的余弦值为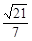 ,求
,求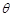 的大小.
的大小.
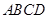 中,
中, 为正三角形,
为正三角形,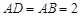 ,
, ,
, 与
与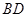 交于
交于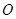 点.将
点.将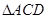 沿边
沿边 折起,使
折起,使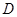 点至
点至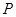 点,已知
点,已知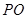 与平面
与平面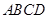 所成的角为
所成的角为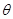 ,且
,且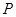 点在平面
点在平面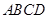 内的射影落在
内的射影落在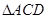 内.
内.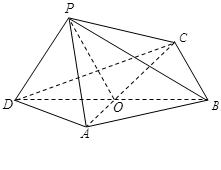
(Ⅰ)求证:
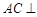 平面
平面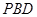 ;
;(Ⅱ)若已知二面角
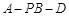 的余弦值为
的余弦值为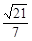 ,求
,求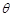 的大小.
的大小.(Ⅰ)只需证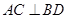 、
、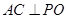 即可;(Ⅱ)
即可;(Ⅱ)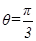 。
。
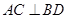 、
、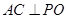 即可;(Ⅱ)
即可;(Ⅱ)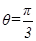 。
。试题分析:(Ⅰ)易知
 为
为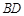 的中点,
的中点,则
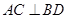 ,又
,又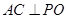 ,
,又
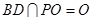 ,
,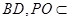 平面
平面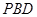 ,
,所以
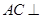 平面
平面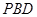 (5分)
(5分)(Ⅱ)方法一:以
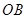 为
为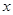 轴,
轴,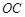 为
为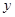 轴,过
轴,过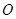 垂直于
垂直于平面
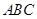 向上的直线为
向上的直线为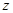 轴建立如图所示空间
轴建立如图所示空间直角坐标系,则
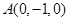 ,
,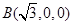
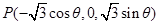 (7分)
(7分)易知平面
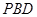 的法向量为
的法向量为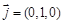 (8分)
(8分)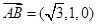 ,
,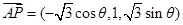 设平面
设平面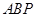 的法向量为
的法向量为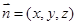
则由
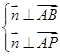 得,
得,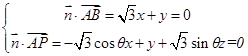
解得,
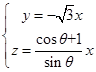 ,令
,令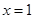 ,则
,则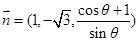 (11分)
(11分)则
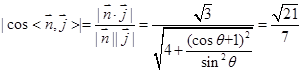
解得,
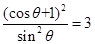 ,即
,即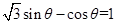 ,即
,即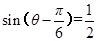 ,
,又
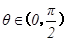 ,∴
,∴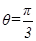 故
故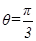 .(15分)
.(15分) 点评:用综合法求二面角,往往需要作出平面角,这是几何中一大难点,而用向量法求解二面角无需作出二面角的平面角,只需求出平面的法向量,经过简单运算即可,从而体现了空间向量的巨大作用.二面角的向量求法: ①若AB、CD分别是二面
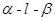 的两个半平面内与棱
的两个半平面内与棱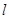 垂直的异面直线,则二面角的大小就是向量
垂直的异面直线,则二面角的大小就是向量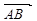 与
与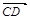 的夹角; ②设
的夹角; ②设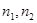 分别是二面角
分别是二面角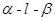 的两个面α,β的法向量,则向量
的两个面α,β的法向量,则向量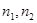 的夹角(或其补角)的大小就是二面角的平面角的大小。
的夹角(或其补角)的大小就是二面角的平面角的大小。
练习册系列答案
相关题目
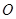 ,设
,设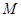 是线段
是线段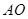 上一点,且
上一点,且 是直角,则
是直角,则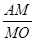 的值为 .
的值为 . 平面PEG.
平面PEG.
 .
. 


 α,n
α,n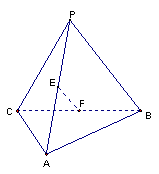
 的侧棱垂直于底面,各顶点都在都在同一球面上,若
的侧棱垂直于底面,各顶点都在都在同一球面上,若 ,则此球的表面积等于
,则此球的表面积等于